图的分类 -- 潘登同学的图论笔记
无向图(我们着重讨论简单图)
图的数学语言
根据前面数据结构的引入, 我们可以清楚的知道:图的由顶点, 边组成;
- 贯彻集合论的思想, 将点写成一个点集V, 边写成一个边集E; $$ V = {v_1,v_2,v_3,...,v_n}\ E = {e_1,e_2,e_3,...,e_m}\ $$
- 还有他们的对应关系呢! 定义一个由$E→V^2$的映射$r$;
$$r(e) = {u,v} \subseteq V$$
所以我们以后就用$G = (V,E,r)$来描述无向图了
接下来是用来描述图的术语
邻接
假设$G = (V,E,r)$为无向图, 若G的两条边$e_1$和$e_2$都与同一个顶点相关联, 则称$e_1$和$e_2$是邻接的
自环,重边
假设$G = (V,E,r)$为无向图,如果存在$e$,有$r(e)={u,v}$且$u=v$, 那么称$e$为一个
自环假设$G = (V,E,r)$为无向图,若G中关联同一对顶点的边多于一条,则称这些边为
重边degree(度)
假设$G = (V,E,r)$为无向图,$v\in V$, 顶点v的度数dgree
deg(v)是G中与v关联的边的数目(说白了就是有多少个顶点跟v相连)孤立顶点, 悬挂点,奇度点,偶度点
假设$G = (V,E,r)$为无向图,G中度数为零的顶点称为
孤立零点,图中度数为1的顶点成为
悬挂点,与悬挂点相关联的边称为悬挂边,图中度数为k的点成为
k度点,度数为奇数的为奇数点,度数为偶数的称为偶数点
简单图:不存在自环和重边的无向图
图的基本定理/握手定理- 假设$G = (V,E,r)$为无向图,则有$\sum deg(v) = 2|E|$; 即所有顶点的度数是边的两倍 > 这个的定理是显然的,因为一条边能连接两个顶点
推论: 在任何无向图中,奇数度的点必为偶数个 > 这个也很好证明,因为总的度数是偶数, 那想所有顶点的度数之和为偶数, 偶数个奇数度的顶点之和才能是偶数
例子: 问题如下: 假设有9个工厂, 求证:
- (1)在他们之间不可能每个工厂都只与其他3个工厂有业务联系
- (2)在他们之间不可能只有4个工厂与偶数个工厂有业务联系 > 证明留给读者喔!
在简单图范畴下的其他有特点的图
- 零图,离散图 > G中全是孤立顶点, 也称0-正则图
- 正则图 > 所有顶点度数都相同的图, 若所有顶点度数均为k, 则称k-正则图
- 完全图 > 任意两个顶点都有边, 也称n-正则图
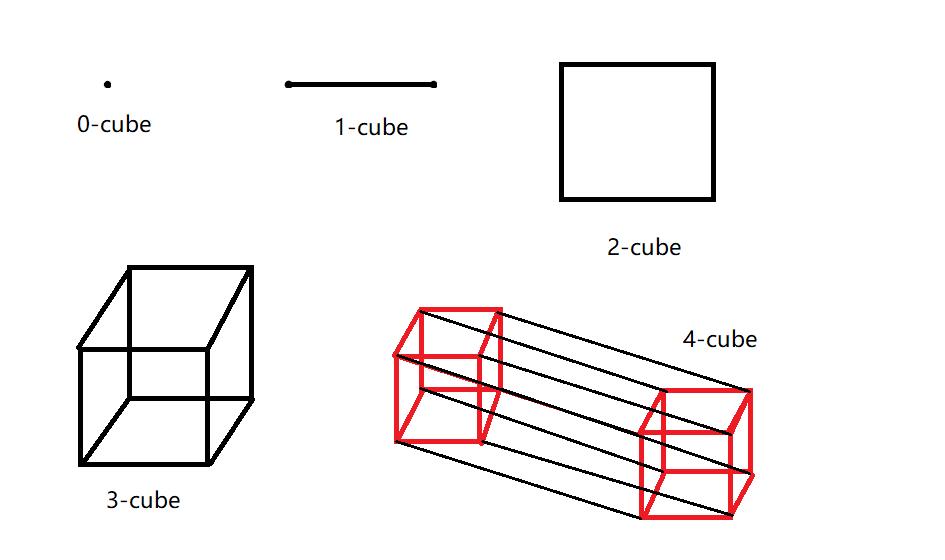
n-立方体图
其实长的就跟立方体一样,但由于图是平面的,下面给出严谨的数学定义 如果图的顶点集v由集合{0,1}上的所有长为n的二进制串组成,两个顶点的相邻当且仅当他们的标号序列仅在一位数字上不同 如图绘制了多个立方体图
大家也可以尝试自己构建(推荐一个构建网络的小工具networkx,但是networkx不是本文的主要工具,故不详细讲解,感兴趣的朋友们自己了解哦)
- 贴上代码
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
points = {'100':['101', '110', '000'],
'110':['111', '100', '010'],
'000':['001', '010', '100'],
'001':['101', '011', '000'],
'011':['001', '111', '010'],
'101':['111', '100', '001'],
'111':['110', '101', '011'],
'010':['110', '011', '000']}
for i in points:
for j in points[i]:
G.add_edge(i, j)
# 设置节点的位置
left = ['100', '110']
middle_left = ['000', '010']
middle_right = ['001', '011']
right = ['101', '111']
options = {
"font_size": 36,
"node_size": 100,
"node_color": "white",
"edgecolors": "black",
"edge_color": 'red',
"linewidths": 5,
"width": 5,
'alpha':0.8,
'with_labels':True
}
pos1 = {n: (0, 5-3*i) for i, n in enumerate(left)}
pos1.update({n: (1, 4-i) for i, n in enumerate(middle_left)})
pos1.update({n: (2, 4-i) for i, n in enumerate(middle_right)})
pos1.update({n: (3, 5-3*i) for i, n in enumerate(right)})
plt.clf()
nx.draw(G, pos1, **options)
一个3-立方体图如下:
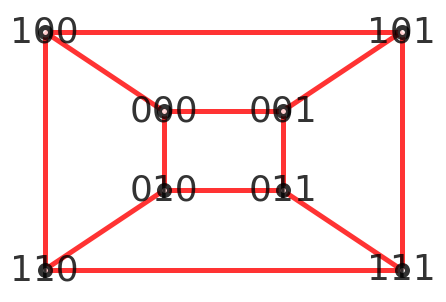
圈图
假设$V = {1,2,...,n} (n>2),E = {(u,v)| 1 ≤ u, v ≤ n, u-v ≡ 1(mods\quad n)}$ 则称简单图为轮图
一个圈图如下:
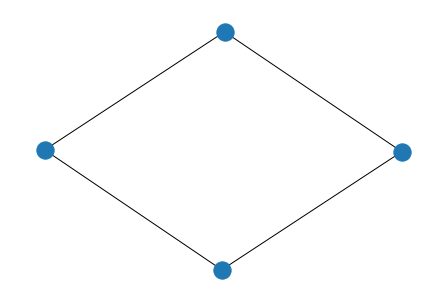
轮图
假设$V = {0,1,2,...,n} (n>2), E = {(u,v)| 1 ≤ u, v ≤ n, u-v ≡ 1(mods\quad n) 或者 u=0, v>0}$ 则称简单图为轮图, 其实就是在圈图的基础上增加了一个顶点去连接所有点
一个轮图如下:
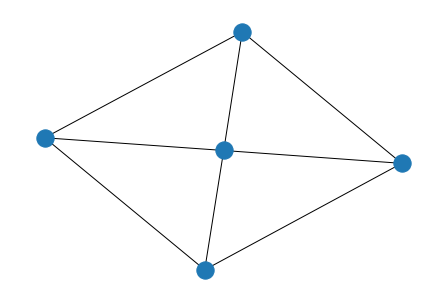
二部图(很经典)
若简单图$G = (V,E,r)$的顶点V存在一个划分${V_1, V_2}$使得G中任意一条边的两端分别属于$V_1$和$V_2$,则称$G$是二部图
如果V1中每个顶点都与V2中每个顶点相邻, 则成为完全二部图
- 一个二部图如下:

- 一个完全二部图如下:

有向图
就是上面的无向图的边有了方向即边$e = {u, v}$是一个有序对
degree(度)
上面已经介绍过度了, 但在有向图中我们要把他细分一下 $deg(v) = deg(v)^{(-)} + deg(v)^{(+)}$
出度: 以v为起始点的有向边的数目, 记为$deg(v)^{(+)}$入度: 以v为终点的有向边的数目, 记为$deg(v)^{(-)}$定理对任意有向图$G=(V,E,r)$, 有$\sum deg(v)^{(-)} = \sum deg(v)^{(+)} = |E|$
赋权图
假设$G=(V,E,r)$为图, $W是E到\mathcal{R}$的一个函数,则称G为赋权图,对于$e\in E,w(e)$称作边e的权重或者简称权
其实就是之前实现图的数据结构中的cost
图的同构与子图
同构
设$G_1 = (V_1,E_1,r_1)$和$G_2 = (V_2,E_2,r_2)$是两个无向图
如果存在$v_1$到$v_2$的双射$f$和$E_1$到$E_2$的双射$g$, 满足对任意的$e\in E_1$,若$r_1(e)={u,v}$,则$r_2(g(e))= {f(u), f(v)}$ ,则称$G_1和G_2$是同构的,并记为$G_1\cong G_2$
一对全等图的图像如下:
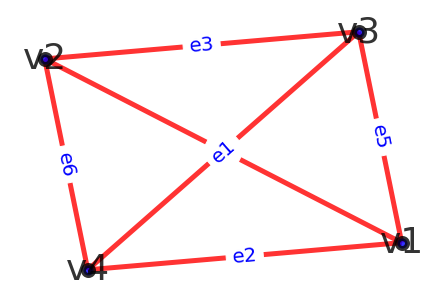

点集之间的双射函数$f(v_1) = a, f(v_2) = b, f(v_3) = c, f(v_4) = d$
边集之间的双射函数$f(e_i) = E_i, i = 1,2,...,6$
补图
假设$G=(V,E)$是一个n阶简单图 令$E' = {(u,v)|u,v\in V, u \neq v, {u,v}\notin E}$ 则称$(V, E')$为G的补图, 记作$G' = (V,E')$
若$G与G'$同构, 则称$G$为自补图
子图
设$G_1 = (V_1,E_1,r_1)$和$G_2 = (V_2,E_2,r_2)$是两个图; 若满足$V_2 ⊆ V_1, E1 ⊆ E2, 及r_2 = r_1|E_2$, 即对于$∀e∈E_2 有r_2(e) = r_1(e)$ ,则称$G_2是G_1$的子图
当$V_1=V_2$时,称$G_2是G_1$的支撑子图(因为当把顶点看成构成这个图的支点,当支点与原本图都一样的时候就可以把他称为支撑子图)
当$E_1 ⊆ E_2$ 或 $V_2 ⊆ V_1$ 时, 称$G_2是G_1$的真子图
当$V_2 = V_1$ 且 $E_2 = E_1$或$E_2 = ∅$时, 称$G_2是G_1$的真子图
导出子图
设$G_2 = (V_2,E_2,r_2)$是$G_1 = (V_1,E_1,r_1)$的子图,若$E_2={e|r_1(e)={u,v}⊆V_2}$(即E2包含了图G中V2的所有边)
构造子图的几种方法
- 在原图中删掉点和与他关联的边,(得到的图也叫删点子图)
- 在原图中删掉边(得到的是删边子图)
道路、回路与连通性
道路
有向图$G=(V,E,r)$中一条道路Π 是指一个点-边序列$v_0,e_1,v_1,...,e_k,v_k$,满足对于所有$i=1,2,...,k$
$r(e_i) = (v_i-1,v_i)$ 称Π是从$v_0$到$v_u$的道路
回路
如果上面的道路中$v_1 = v_k$, 就是回路
简单道路/简单回路
如果道路/回路中各边互异,则称Π是简单道路/简单回路
如果道路/回路中,除$v_0,v_k$外,每个顶点出现一次, 则称$Π$是初级道路/初级回路(也称圈)
定理
假设简单图G中每个顶点的度数都大于1,则G中存在回路
证明: 假设$Π:v_0, v_1, ... ,v_{k-1},v_k$是图G中最长的一条初级道路,显然$v_0$和$v_k$都不会与不在道路$Π$上的任何顶点相邻,否则就会有一条更长的道路;
但是,$deg(v_0)>1$,因此必定存在$Π$上的顶点$v_i$与$v_0$相邻,于是产生了回路
可达
u,v是G中两个顶点,如果u=v或G中存在u到v的道路,则称u到v是可达的
连通图
假设G是无向图,如果图中任意两相异点之间都存在道路,则称G是连通的或者连通图
连通分支(重要)假设无向图$G=(V,E)$的顶点集V在可达关系下的等价类为${v_1, v_2, ..., v_k}$,则G关于$v_i$的导出子图称作G的一个连通分支(其中$i=1,2,...,k$)
如果形象理解连通分支呢? 我举一个通俗一点的例子好了
就拿国家与国家之间的关系来理解好了, 一个国家可能有很大的疆域也可能只有很小的疆域; 但是在与其他的国家进行外交的时候,无论这个国家再小,都是以一个独立的身份与别国外交; 而无论某个国家的某个地区的实力再强大,也不能独立的与别国外交(即一个国家只会一个身份去与别国外交);
而连通分支就是来描述这样一种情况, 在一个网络中, 有很多的顶点, 但是很多顶点都有共性(比如他们500年前是一家), 那么就可以把他们看成一个顶点,这样就方便分析了
而这个共性具体来说就是;
互相可达(就是这一堆的任何顶点都可以达到另一个顶点(也要在网络内))
后面还会讲到怎么求解连通分支的kosaraju算法
- 一个包含三个连通分支的图如下:

割边(桥)
假设$G=(V,E,r)$是连通图, 若$e∈E$,且$G-e(从G中去掉边e)$不连通,则称$e$是图$G$中的一条割边或桥
如上图的7→9就是桥, 因为去掉之后图就不连通了
定理连通图中的边e是桥, 当且仅当e不属于图中任意的一条回路;(因为回路一定是有来又回,如果桥在回路里面,那把他去掉图仍然是连通的)
有向图的连通
假设G是有向图,如果忽略图中边的方向后得到的无向图是连通的,则称G为连通的;否则就是不连通的
强连通, 单向连通
有向连通图G, 对于图中任意两个顶点u和v,u到v 和 v到u都是可达的,则称G为强连通的; 如果图中任意两个顶点u和v, u到v 和 v到u至少之一是可达的,则称G为单向连通的
有向无环图(DAG)
有向图G,如果图中不存在有向回路,则称G为有向无环图
欧拉图
- 欧拉图
其实欧拉图的来源是那个柯尼斯堡七桥问题,这不是本文重点,感兴趣的同学自行百度喔
通过图G中每条边一次且仅一次的道路称作该图的一条欧拉道路;(相当于一笔画)
通过图G中每条边一次且仅一次的回路称作该图的一条欧拉回路;(相当于头尾相连的一笔画)
存在欧拉回路的图称作欧拉图
- 一些例子如下:
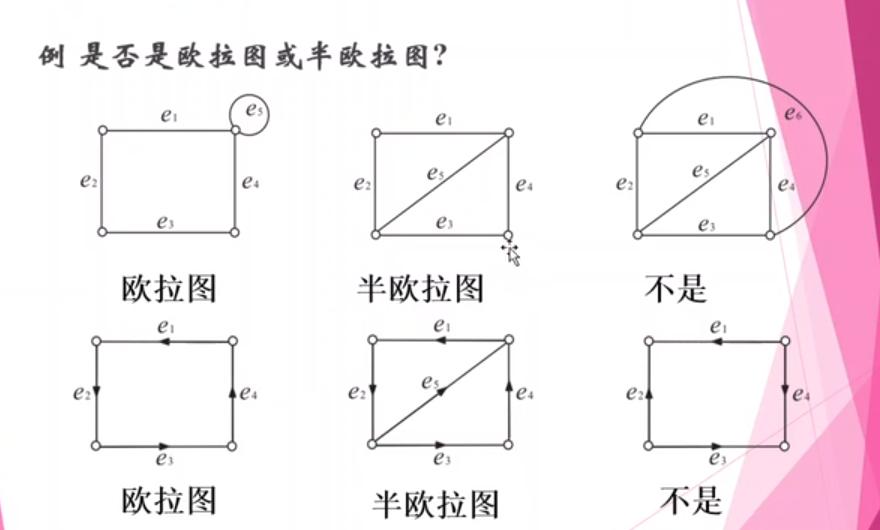
欧拉图的充要条件> 无向图G是欧拉图当且仅当G是连通的而且所有顶点都是偶数度
证明: (必要性)假设G是欧拉图,即图中有欧拉回路,即对于任意一个顶点,有入必有出,因此每个顶点都是偶数度;
(充分性)设G的顶点是偶数度, 采用构造法证明欧拉回路的存在性:
从任意点v0出发,构造一条简单回路C, 因为各顶点的度数都是偶数, 因此一定能够回到v0, 构造简单回路;(!!!想清楚了再往下看!!!)
下一步,在上面构造的简单回路中挑一点在剩余的点和边中构造简单回路,重复该过程,直到不能再构造为止.
定理> 无向图G存在欧拉道路当且仅当G是连通的而且G中奇数度顶点不超过两个
证明: (必要性)G中一条欧拉道路L,在L中除起点和终点之外,其余每个顶点都与偶数条边(一条入,一条出)相关联. 因此, G中至多有两个奇数度的顶点
(充分性) ①若G中没有奇数度的顶点u,v,由上面定理,存在欧拉回路,显然是欧拉道路
②若G中有两个奇数度顶点u,v,那么连接uv,根据上面定理,可知存在一个欧拉回路C,从C中去掉边uv,得到顶点为u,v的一条欧拉道路(当我证到这的时候,应该有妙蛙妙蛙的声音)
(算法)构造欧拉回路 Fleury(G)
前提:得存在
输入: 至多有两个奇数度顶点的图G=(V,E,r)
输出:以序列的形式呈现欧拉回路/道路Π
算法流程:
① 选择图中一个奇数度的顶点v∈V,如果图中不存在奇数度顶点,则任取一个顶点v, 道路序列Π←v
② $while |E| ≠ 0$
- if 与v关联的边多余一条,则任取其中不是桥的一条边e:
- else 选择该边e:
- 假设e的两个端点是$v,u, Π←Π·e·u, v←u$
- 删除边e及孤立顶点(如果有)
- ③ 输出序列
定理
假设连通图G中有k个度为奇数的顶点,则G的边集可以划分成$k/2$条简单道路,而不能分解为$(k/2 - 1)$或更少条道路
证明: (前半句) 由握手定理知k必为偶数.将这k个顶点两两配对,然后增添互不相邻的$k/2$条边,得到一个无奇数度顶点的连通图$G'$,
那么由前面的定理知,$G'$存在欧拉回路$C$,在$C$中删去增添的$k/2$条边, 便得到了$k/2$条简单道路;
(后半句) 假设图G的边集可以分为q条简单道路,则在图G中添加q条边可以得到欧拉图G',因此图中所有顶点都是偶数度,而每添加一条边最多可以把两个奇数度顶点变为偶数度,即$2q≥k$
- 无向图的欧拉道路--推广-->有向图
定理> 有向图G中存在欧拉道路当且仅当G是连通的,而且G中每个顶点的入度都等于出度; > > 有向图G中存在欧拉道路,但不存在欧拉回路当且仅当G是连通的; > > 除两个顶点外,每个顶点的入度都等于出度,而且这两个顶点中一个顶点的入度比出度大1,另一个的入度比出度小1;
哈密顿图
哈密顿图
图中含有
哈密顿回路的图哈密顿道路
通过图G中每个顶点一次且仅一次的道路称作该图的一条哈密顿道路;
哈密顿回路
通过图G中每个顶点一次且仅一次的回路称作该图的一条哈密顿回路;
注意1.图G中存在自环/重边不影响哈密顿回路/道路的存在性
2.哈密顿图中一定不存在悬挂边
3.存在哈密顿道路的图中不存在孤立顶点
例子: 科学家排座问题
由七位科学家参加一个会议,已知A只会讲英语;B会讲英、汉;C会讲英、意、俄;D会日、汉;E会德、意;
F会法、日、俄;G会讲德、法;安排他们坐在一个圆桌,使得相邻的科学家都可以使用相同的语言交流;
这就是一个很经典的哈密顿图的例子,转换一下,就是把他们之间的关系用图来表示,再在图中找一条哈密顿回路;
将讲相同语言的科学家之间连一条边,构造图,如下:
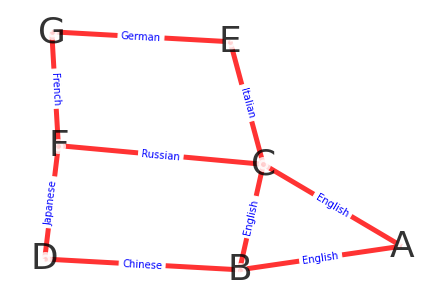
构图代码
# %%科学家排座问题
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
a_dict = {'A':['English'],
'B':['English', 'Chinese'],
'C':['English', 'Italian', 'Russian'],
'D':['Japanese', 'Chinese'],
'E':['German', 'Italian'],
'F':['French', 'Japanese', 'Russian'],
'G':['German', 'French']}
# 用于储存相邻节点, key是语言, value是people_name
neighbors_dict = {}
for people_name in a_dict:
G.add_node(people_name)
for language in a_dict[people_name]:
# 如果这个语言在neighbors_dict, 那么就把会这门语言的其他人
# 与这个人之间连接一条边, 否则就把这个人会的语言加到dict中
if language in neighbors_dict:
for people_name_exist in neighbors_dict[language]:
G.add_edge(people_name_exist, people_name, language=language)
neighbors_dict[language].append(people_name)
else:
neighbors_dict[language] = [people_name]
options = {
"font_size": 36,
"node_size": 100,
"node_color": "white",
"edgecolors": "white",
"edge_color": 'red',
"linewidths": 5,
"width": 5,
'alpha':0.8,
'with_labels':True
}
pos = nx.spring_layout(G)
plt.clf()
nx.draw(G, pos, **options)
# 显示edge的labels
edge_labels = nx.get_edge_attributes(G, 'language')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=10, font_color='blue')
再寻找一条回路经过所有顶点,这里我们采用DFS(深度优先搜索)
DFS深度优先搜索
DFS的本质是暴力搜索算法,也称回溯算法,就是一种在找不到正确答案的时候回退一步,再继续向前的算法
算法的思想很简单,但是实际操作可能会有点不好理解;下面我们通过几个小案例来深入理解DFS算法
- 例子1: > 全排列问题: 给出一个数字n,要求给出1-n的全排列,输出结果为列表
如给定数字3, 那结果就是[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
上代码!!!
# 回溯算法
def template(n): # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
result = [] # 这个保存结果
def trace(path, choices): # 递归函数
'''
path: 用于储存目前排列
choices: 用于储存所有可选择的数字(1-n)
'''
if len(path) == n: # 当path的长度等于输入的n时,结束算法,把结果加入结果列表
result.append(list(path))
return
for item in choices:
if item in path: # 减枝操作(如果path里面有item这个数)
continue
path.append(item) # 如果没有就把他加到目前的path中
trace(path, choices) # 递归调用自身
path.pop() # 撤销最后一次的选择继续向前找答案
trace([], range(1, n+1)) # 调用函数trace
return result
if __name__ == '__main__':
print(template(3))
观察到输出结果与上面预期一致,(回溯算法是后面很多算法的基础)
- 例子2: > 给定一个55的矩阵,里面有零元素,要求在矩阵里面5个0,使得每一行每一列都有零 > > [[7, 0, 2, 0, 2],[4, 3, 0, 0, 0],[0, 8, 3, 5, 3],[11, 8, 0, 0, 4],[0, 4, 1, 4, 0]]
上代码!!!
#%%矩阵找零
import copy
def template(matrix): # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
result = [] # 这个保存结果
def trace(path, choices): # 递归函数
'''
path: dict 用于储存找到的零 key表示row values表示column
choices: 矩阵matrix
'''
if len(path) == len(matrix): # 当path的长度等于输入的n时,结束算法,把结果加入结果列表
if path not in result:
result.append(copy.deepcopy(path))
return
for row, items in enumerate(choices):
for column, j in enumerate(items):
if j == 0: # 当元素为零时
if row in path.keys():
continue
if column in path.values(): # 减枝操作(如果path里面有column,说名这一列已经有零了)
continue
path[row] = column # 如果没有就把他加到目前的path中
trace(path, choices) # 递归调用自身
path.popitem() # 撤销最后一次的选择继续向前找答案
trace({}, matrix) # 调用函数trace
return result
if __name__ == '__main__':
matrix = [[7, 0, 2, 0, 2],
[4, 3, 0, 0, 0],
[0, 8, 3, 5, 3],
[11, 8, 0, 0, 4],
[0, 4, 1, 4, 0]]
print(template(matrix))
可以看到最终返回了两个结果:
[{0: 1, 1: 2, 2: 0, 3: 3, 4: 4}, {0: 1, 1: 3, 2: 0, 3: 2, 4: 4}]
表示的就是第0行选择第1列,第1行选择第2列,第2行选择第0列,第3行选择第3列,第4行选择第4列;带回矩阵验证发现符合条件
其实可以把例子2中的问题转换一下,又变成一个排列问题,仍然采用相同的方法求解
- 例子2(变形): > 在[2,4],[3,4,5],[1],[4,5],[1,5]中找到1-5的一个排列(如2,3,1,4,5) > > 把所有可能的结果输出成列表
上代码!!!
#%%将矩阵找零问题转化
import copy
def template(a):
result = []
def trace(path,choices):
if len(path) == len(choices):
if path not in result:
result.append(copy.deepcopy(path))
return
for row, items in enumerate(choices):
if len(path) != row: # path的元素的index对应choice的第几行
continue # 要是没有这一个if判断,path中储存的元素会乱
for j in items:
if j in path:
continue
path.append(j)
trace(path,choices)
path.pop() #删掉最后一个元素
trace([],a)
return result
if __name__ == '__main__':
a = [[2,4],[3,4,5],[1],[3,4],[1,5]]
print(template(a))
可以看到结果是一致的
- 例子3:给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合
上代码!!!
#%%77. 组合
# 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
class Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
result = []
def trace(path, choices, k):
if len(path) == k:
path = sorted(path)
if path not in result:
result.append(path)
return
for items in choices:
if items in path:
continue
path.append(items)
trace(path,choices, k)
path.pop()
trace([], range(1, n+1), k)
return result
if __name__ == '__main__':
print(Solution().combine(4, 2))
可以看到结果符合题意
经过上面几个例子的引入,同学们对回溯算法应该比较了解了,现在我们来完成科学家的排座问题吧!
科学家排座问题
- 修改数据结构,因为在DFS中要从一个点出发,遍历所有节点,为避免重复,对节点的数据结构加上color这个属性,标识为
white, - 对应的新增方法来修改color,以及查看color, 当节点已经被走过来就把他标识为
gray,就不会再去遍历他;
话不多说,上代码!!!
#%% 科学家排座问题
from Vertex import Vertex # 导入Vertex
from Graph import Graph # 导入之前实现的Graph
class New_Vertex(Vertex): # 某一个具体问题的数据结构需要继承原有数据结构
def __init__(self, key):
super().__init__(key)
self.color = 'white' # 新增类属性(用于记录节点是否被走过)
# 新增类方法, 设置节点颜色
def setColor(self, color):
self.color = color
# 新增类方法, 查看节点颜色
def getColor(self):
return self.color
class New_Graph(Graph): # 继承Graph对象
def __init__(self):
super().__init__()
# 重载方法 因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
def addVertex(self, key): # 增加节点
'''
input: Vertex key (str)
return: Vertex object
'''
self.numVertices = self.numVertices + 1
newVertex = New_Vertex(key) # 创建新节点
self.vertList[key] = newVertex
return newVertex
# 新增方法
def addUndirectedEdge(self, key1, key2, cost=1):
self.addEdge(key1, key2, cost)
self.addEdge(key2, key1, cost=1)
class Solution(): # 解决具体问题的类对象
# 对科学家们创建图,之前有过相关操作
def createGraph(self, a_dict):
'''
input: a_dict type: dict, key: people_name, value: language
return: graph
'''
# 创建图
graph = New_Graph()
# 用于储存相邻节点, key是语言, value是people_name
neighbors_dict = {}
for people_name in a_dict:
graph.addVertex(people_name)
for language in a_dict[people_name]:
# 如果这个语言在neighbors_dict, 那么就把会这门语言的其他人
# 与这个人之间连接一条边, 否则就把这个人会的语言加到dict中
if language in neighbors_dict:
for people_name_exist in neighbors_dict[language]:
graph.addUndirectedEdge(people_name_exist, people_name)
neighbors_dict[language].append(people_name)
else:
neighbors_dict[language] = [people_name]
return graph
# 关键函数DFS,有
def DFS(self, g, start):
result = []
# 深度优先搜索
def trace(path, g, start): # path是探索的路径 g是图,start是起始的节点
start.setColor('gray') # 将正在探索的节点设置为灰色
path.append(start)
# path中包含了所有顶点,且最后一个顶点到初始顶点要有路径就是最终结果
if len(path) == len(g):
if path[-1] in path[0].getConnections():
result.append(list(path))
return
else:
for i in list(start.getConnections()):
if i.getColor() == 'white': # 如果与他相邻的顶点还是白色,就探索他
trace(path, g, i)
path.pop()
i.setColor('white') # 将已经撤销的结果的节点设置回白色
trace([], g, start)
return result
if __name__ == '__main__':
a_dict = {'A':['English'],
'B':['English', 'Chinese'],
'C':['English', 'Italian', 'Russian'],
'D':['Japanese', 'Chinese'],
'E':['German', 'Italian'],
'F':['French', 'Japanese', 'Russian'],
'G':['German', 'French']}
s = Solution()
graph = s.createGraph(a_dict)
path = s.DFS(graph, graph.getVertex('A'))
# 因为是无向图,如果存在一个回路那一定会有两条路径
for n in range(len(path)):
for i in path[n]:
print(i.getId(), end='-')
print('\t')

看到最后输出了两个结果,表示科学家两两的相邻关系,带回题目,发现OK!!!
平面图
平面图
如果可以将无向图G画在平面上,使得除端点处外,各边彼此互不相交,则称G是具有平面性的图(简称平面图)
欧拉公式$面f、边m、顶点数n,的关系$
设G是一个面数为$f(n,m)$-连通平面图,则有 $$n-m+f = 2$$
当然啦,欧拉公式已经像呼吸一样被我们所接受了,所以我这里就不证这种(1+1=2)的证明了,放一个链接:
推论> 设G是一个面数为f的(n,m)平面图,且有L个连通分支,则 > $$n-m+f = L+1$$
证明: 假设这$L$个分支是$G_1,G_2, ... ,G_L$,并设$G_i$的顶点数、边数和面数分别为$n_i,m_i和f_i$;
显然有$\sum n_i = n$和$\sum m_i = m$; 此外, 由于外部面是各个连通分支共用的,因此$\sum f_i = f + L - 1$
由于每个Gi都是连通图,因此由欧拉公式有$n_i - m_i + f_i = 2$
于是有$n - m + f = ∑n_i + ∑m_i + ∑f_i + 1 - L = ∑(n_i - m_i + f_i) + 1 - L = 2L + 1 - L = L + 1$
e的细分
假设$G=(V,E,r)$是无向图, $e∈E$,顶点u与v是边e的两端,e的细分是指在G中增加一个顶点w,删去边e,新增以u和w为端点的边$e_1$以及w和v为端点的边$e_2$
就相当于原本有俩城市直接相连,然后现在找一个中继点,把这俩城市通过这个中继点连接
库拉托夫斯基定理一个无向图是平面图当且仅当他不包含与
k5(5阶完全图) 或k3,3(完全3,3二部图)的细分同构子图例子:
- 求证: 彼得森图不是平面图 > 先介绍一下彼得森图,是一个由10个顶点和15条边构成的连通简单图,它一般画作五边形中包含有五角星的造型。
一个经典的彼得森图如下:

我们采用构图法证明:
左图是一个彼得森图,把中间的O点去掉,得到一个彼得森图的子图.
将这个子图看成一个K3,3的细分同构 (由K3,3构造中间的图的方式是: 去掉边BC,增加顶点A,去掉边DH、EI, 增加顶点F, G)
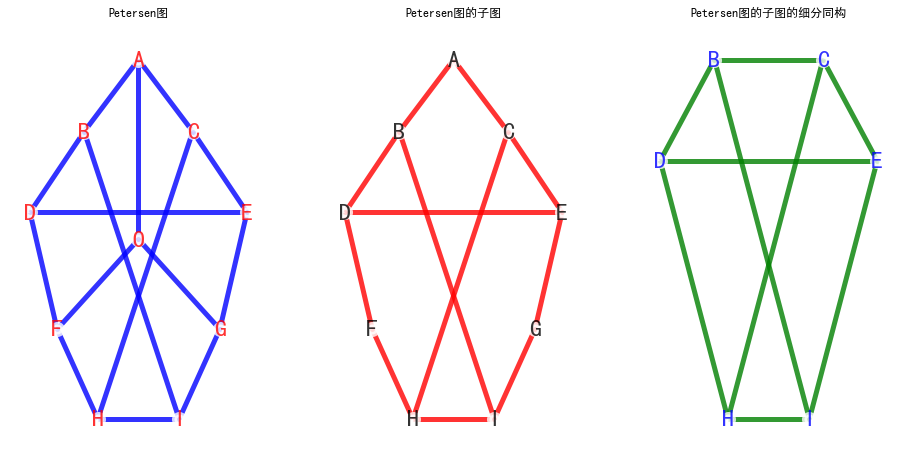
- 上图代码
#%%彼得森图不是平面图的证明
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
G = nx.Graph()
points = {'A':['B', 'C', 'O'],
'B':['A', 'D', 'I'],
'C':['A', 'E', 'H'],
'D':['B', 'E', 'F'],
'E':['C', 'D', 'G'],
'F':['D', 'H', 'O'],
'G':['E', 'I', 'O'],
'H':['F', 'I', 'C'],
'I':['G', 'H', 'B'],
'O':['A', 'G', 'F']}
for i in points:
for j in points[i]:
G.add_edge(i, j)
points_1 = ['A']
points_2 = ['B', 'C']
points_3 = ['D', 'E']
points_4 = ['F', 'G']
points_5 = ['H', 'I']
points_6 = ['O']
options = {
"font_size": 24,
"node_size": 100,
"node_color": "white",
"edgecolors": "white",
"edge_color": 'blue',
"font_color": 'red',
"linewidths": 5,
"width": 5,
'alpha':0.8,
'with_labels':True
}
pos = {n: (2, 5) for i, n in enumerate(points_1)}
pos.update({n: (1+2*i, 4.2) for i, n in enumerate(points_2)})
pos.update({n: (4*i, 3.3) for i, n in enumerate(points_3)})
pos.update({n: (0.5+3*i, 2) for i, n in enumerate(points_4)})
pos.update({n: (1.25+1.5*i, 1) for i, n in enumerate(points_5)})
pos.update({n: (2, 3) for i, n in enumerate(points_6)})
plt.figure(figsize=(16,8))
plt.subplot(131)
nx.draw(G, pos, **options)
G.remove_node('O')
plt.title('Petersen图')
plt.subplot(132)
pos.pop('O')
options['edge_color'] = 'red'
options['font_color'] = 'black'
nx.draw(G, pos, **options)
plt.title('Petersen图的子图')
plt.subplot(133)
G3_3 = G = nx.Graph()
points3_3 = {'B':['D', 'C', 'I'],
'C':['B', 'E', 'H'],
'D':['B', 'E', 'H'],
'E':['C', 'D', 'I'],
'H':['C', 'D', 'I'],
'I':['E', 'H', 'B']}
for i in points3_3:
for j in points3_3[i]:
G3_3.add_edge(i, j)
pos1 = {n: (1+2*i, 4.2) for i, n in enumerate(points_2)}
pos1.update({n: (4*i, 3.3) for i, n in enumerate(points_3)})
pos1.update({n: (1.25+1.5*i, 1) for i, n in enumerate(points_5)})
options['edge_color'] = 'green'
options['font_color'] = 'blue'
nx.draw(G3_3, pos1, **options)
plt.title('Petersen图的子图的细分同构')
可平面图与哈密顿图存在联系
如果简单图G既是哈密顿图又是平面图,那么在G画为平面图后,
G的不在哈密顿回路C中的边落在两个集合之一: C的内部或C的外部
(算法)哈密顿图的可平面性判断算法 QHPLanar(G)
输入: (n, m)-简单哈密顿图G
输出: True or False
① 将图G的哈密顿回路哈在平面形成一个环,使得C将平面划分为内部区域和外部区域
② 设G的不在C中的边$e_1,e_2,...,e_{m-n}$, 在新的图$G'$中构造顶点(顶点就是这个m-n个)
③ 若$e_i和e_j$在G的新画法中必须是交叉的,即他们二者无法同时画在C的内部或者外部,则在图$G'$的顶点$e_i和e_j$中连一条边
④ 若$G'$是二部图, 则输出T, 否则输出F
因为涉及到了两个边的画法问题,潘登同学暂时不能做算法实现0.0算法例子: (判断G是否可平面)
左图是题目图G,判断是否可平面
中图是将图G画在平面上形成一个环, 右图是将e构造顶点形成新的图
发现新的图是一个二部图, 所以G可平面
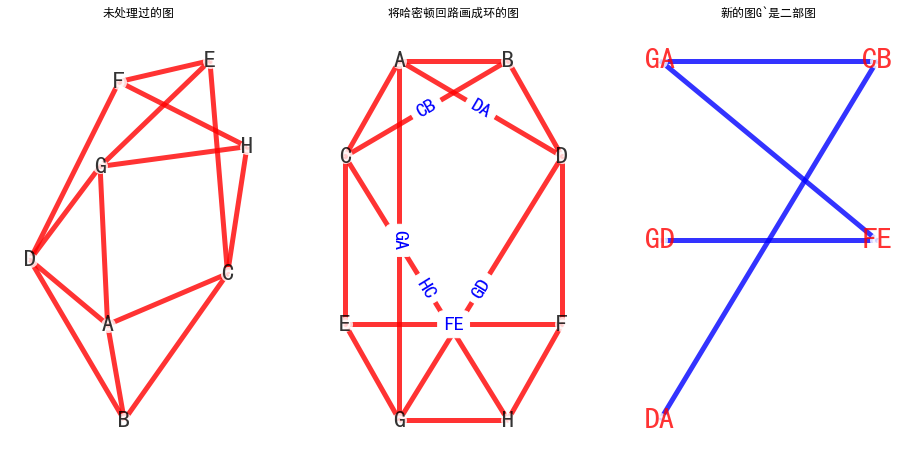
- 上图代码
#%%可平面性的判定例子
G = nx.Graph()
points_1 = {'A':['B', 'C', 'D', 'G'],
'B':['A', 'D', 'C'],
'C':['A', 'E', 'B'],
'D':['B', 'A', 'F', 'G'],
'E':['C', 'F', 'G'],
'F':['D', 'E', 'H'],
'G':['E', 'A', 'D', 'H'],
'H':['G', 'F', 'C']}
# 用于显示边
G_edge = nx.Graph()
points_edge = {'A':['D', 'G'],
'B':['C'],
'C':['B'],
'D':['A', 'G'],
'E':['F',],
'F':['E',],
'G':['A', 'D',],
'H':['C']}
G_bin = nx.Graph()
points_bin = {'GA': ['CB', 'FE'],
'GD': ['FE'],
'DA': ['CB']}
for i in points_1:
for j in points_1[i]:
G.add_edge(i, j)
for i in points_edge:
for j in points_edge[i]:
G_edge.add_edge(i, j, name=i + j)
for i in points_bin:
for j in points_bin[i]:
G_bin.add_edge(i, j)
points_1 = ['A', 'B']
points_2 = ['C', 'D']
points_3 = ['E', 'F']
points_4 = ['G', 'H']
pos = {n: (1+i, 5) for i, n in enumerate(points_1)}
pos.update({n: (0.5+2*i, 4.2) for i, n in enumerate(points_2)})
pos.update({n: (0.5+2*i, 2.8) for i, n in enumerate(points_3)})
pos.update({n: (1+i, 2) for i, n in enumerate(points_4)})
options = {
"font_size": 24,
"node_size": 100,
"node_color": "white",
"edgecolors": "white",
"edge_color": 'red',
"font_color": 'black',
"linewidths": 5,
"width": 5,
'alpha':0.8,
'with_labels':True
}
plt.figure(figsize=(16, 8))
plt.subplot(131)
nx.draw(G, **options)
plt.title('未处理过的图')
plt.subplot(132)
nx.draw(G, pos, **options)
edge_labels = nx.get_edge_attributes(G_edge, 'name')
nx.draw_networkx_edge_labels(G_edge, pos, edge_labels=edge_labels,
font_size=20, font_color='blue')
plt.title('将哈密顿回路画成环的图')
plt.subplot(133)
points_bin1 = ['GA', 'GD', 'DA']
points_bin2 = ['CB', 'FE']
pos_bin = {n: (1, 5-2*i) for i, n in enumerate(points_bin1)}
pos_bin.update({n: (3, 5-2*i) for i, n in enumerate(points_bin2)})
options_bin = {
"font_size": 30,
"node_size": 100,
"node_color": "white",
"edgecolors": "white",
"edge_color": 'blue',
"font_color": 'red',
"linewidths": 5,
"width": 5,
'alpha':0.8,
'with_labels':True
}
nx.draw(G_bin, pos_bin, **options_bin)
plt.title('新的图G`是二部图')
- 对偶图 > 设G是一个平面图,满足下列条件的图$G'$称为G的对偶图 > > + G的面$f$与$G'$的顶点$V'$ 一 一对应 > + 若G中的面$f_i$和$f_j$邻接于共同边界e,则在$G$'中有与e一一对应的边$e'$,其以$f_i$和$f_j$所对应的点$v_i'$和$v_j'$为两个端点 > + 若割边e处于$f$内,则在$G'$中$f$所对应的点v有一个自环$e’$与$e$一一对应
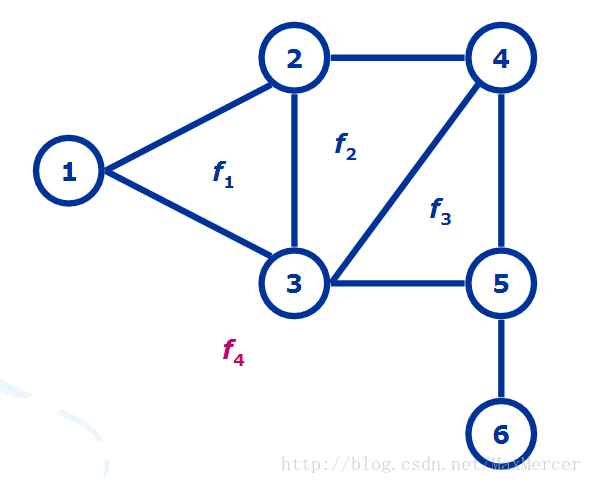
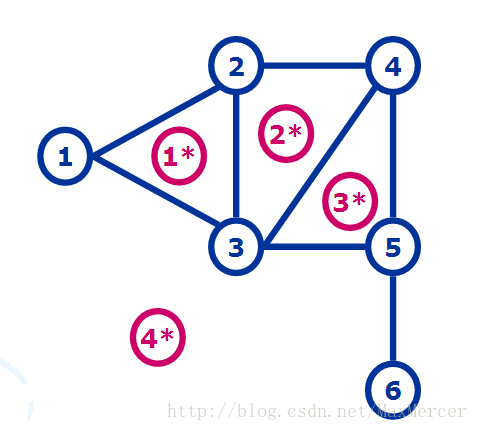
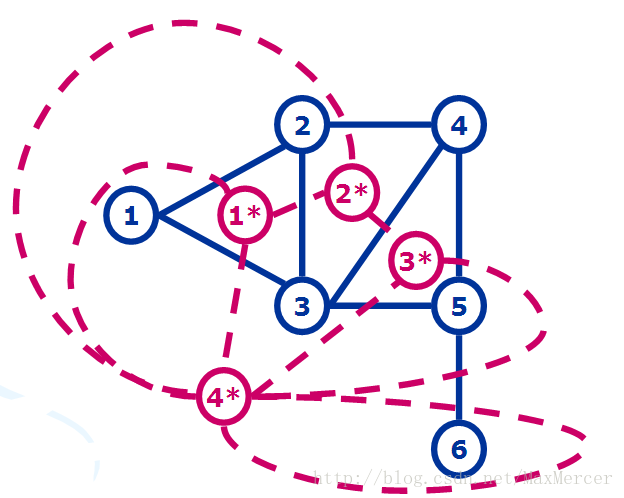
下面是几个对偶图的图:

对偶图的画法> ①在图G中每个面内画一个顶点 > > ② 在这些新的顶点之间添加边,每条新的边恰好与G中一条边相交一次
下面是一个例子:
我们看到对偶图中出现了一个自环, 然后回去看原图的桥,发现就是那一个仅有的桥造成了这个自环
(注: G的桥与G'的自环, G的自环与G'的桥 存在对应关系)
- 图的平面性的应用: > 高速公路的设计 > 电路印刷板的设计中避免交叉
图的分类就是这么多了,继续学习下一章吧!