图的着色 -- 潘登同学的图论笔记

• 图的着色 > 对简单图G的每个顶点赋予一种颜色使得相邻的顶点颜色不同，称图G的一种点着色。对简单图G进行点着色所需的最少颜色数称为G的点色数，记为$χ(G)$

（注：对于n阶简单图，显然有$χ(G)≤n$）

• 边着色

  对简单图G的每条边赋予一种颜色，使得相邻边颜色不同,称为图G的一种边着色

• 面着色

  对无桥平面图图G的每个面赋予一种颜色,使得相邻的面颜色不同，称为图G的一种面着色

(利用对偶图，可以把平面图G的面着色问题转化为研究对偶图G'的点着色问题； 而通过下面的线图概念，也可以将图的边着色问题转化为点着色问题)

• 线图

  假设G是简单图，构造图$L（G）$，G中的边和$L（G）$中的顶点一 一对应 ，如果G中的边$e_1和e_2$相邻，则L（G）中与$e_1和e_2对应的两个顶点间连一条边，称L（G）是G的线图

• 例子： (a)χ(G)=1 当且仅当G是离散图

(b)χ(Kn) = n

(c)(圈图)χ(Cn) = 2, n是偶数时， χ(Cn) = 3，n是奇数时 （n≥3）

(d)(轮图)χ(Wn) = 3 ，n是偶数时， χ(Wn) = 4，n是奇数时 （n≥3）

(e)χ(Gn)=2 当且仅当G是二部图

而点着色问题是NP完全问题Non-deterministic Polynomial，尚不存在有效的方法求解

（给出近似算法）

• (算法)韦尔奇-鲍威尔算法 Welch_Powell（G）

输入: 简单图

输出：图G的一个着色方案

①将图中顶点按度数不增的方式排成排列

②使用一种新颜色对序列的一个顶点进行着色，并且按照序列次序，对与已着顶点不相邻的每一顶点着同样颜色，直至序列末尾。然后从序列中去掉已着色的顶点，得到一个新的序列

③对新序列重复步骤② ， 直至得到空序列

上代码!!!

#%%韦尔奇-鲍威尔算法
import networkx as nx
import matplotlib.pyplot as plt
from Vertex import Vertex
from Graph import Graph
import matplotlib as mpl

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.degree = 0   # 新增类属性(用于节点排序)
        self.color = 'white'  # 新增类属性(用于记录节点的颜色)

    # 重写类方法
    def addNeighbor(self, nbr, weight=0):   # 增加相邻边，默认weight为0
        '''
        input:
            nbr: Vertex object
            weight: int
        return:
            None
        '''
        self.connectedTo[nbr] = weight
        self.degree += 1

    # 新增类方法 (查看degree)
    def getDegree(self):
        return self.degree

    # 新增类方法, 设置节点颜色
    def setColor(self, color):
        self.color = color

    # 新增类方法, 查看节点颜色
    def getColor(self):
        return self.color

class colorGraph(Graph):
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

# 队列数据结构
class Queue():
    def __init__(self):
        self.queue = []

    def enqueue(self, item):
        self.queue.append(item)

    def dequeue(self):
        return self.queue.pop(0)

    def isEmpty(self):
        return self.queue == []

    def size(self):
        return len(self.queue)

    def __iter__(self):
        return iter(self.queue)

    # 查看队首元素
    def see(self):
        return self.queue[0]

class Solution():
    def createGraph(self, a_dict):
        graph = colorGraph()
        for i in a_dict:
            for j in a_dict[i]:
                graph.addEdge(i, j)
        return graph

    # 排序算法 -快速排序
    def quickSort(self, a_list):
        if len(a_list) <= 1:  # 有可能出现left或者right是空的情况
            return a_list
        else:
            mid = a_list[len(a_list)//2]
            left = []
            right = []
            a_list.remove(mid)
            for i in a_list:
                if i[1] > mid[1]:
                    right.append(i)
                else:
                    left.append(i)
            return self.quickSort(left) + [mid] + self.quickSort(right)

    def Welch_Powell(self, g):
        queue = Queue()
        Vertices_keys = g.getVertices()
        Vertices_obj = [g.getVertex(k) for k in Vertices_keys]
        # 用于储存顶点和他的degree
        Vertices_deg = [[i, i.getDegree()] for i in Vertices_obj]
        # 对Vertices_deg进行排序, 然后扔进队列里
        for i in self.quickSort(Vertices_deg)[::-1]:
            queue.enqueue(i[0])
        # 当队列非空
        color = 0  # 颜色标记
        # 已着色顶点
        color_done_vertex = []
        while not queue.isEmpty():
            # 对第一个点进行着色
            frist_vertex = queue.dequeue()
            frist_vertex.setColor(color)
            color_done_vertex.append(frist_vertex)
            for _ in range(queue.size()):
                # 如果color_done_vertex与i这个节点有连接
                Connections = []
                for k in color_done_vertex:
                    Connections += list(k.getConnections())
                if queue.see() in Connections:
                    # 将节点从队首加到队尾
                    queue.enqueue(queue.dequeue())
                else:
                    temp = queue.dequeue()
                    temp.setColor(color)
                    color_done_vertex.append(temp)
            color += 1
        # 输出结果
        result = []
        while Vertices_obj:
            temp_vertex = Vertices_obj.pop()
            result.append((temp_vertex.getId(), temp_vertex.getColor()))
            print(temp_vertex.getId(), ' 的颜色是:', temp_vertex.getColor())
        return result

if __name__ == '__main__':
    a_dict = {'a':['b', 'g', 'h'],
              'b':['a', 'd', 'g', 'h'],
              'c':['d', 'e'],
              'd':['b', 'c', 'f'],
              'e':['c', 'f'],
              'f':['d', 'e'],
              'g':['a', 'b', 'h'],
              'h':['a', 'b', 'g']}
    s = Solution()
    graph = s.createGraph(a_dict)
    result = s.Welch_Powell(graph)

    G = nx.Graph()
    for i in a_dict:
        for j in a_dict[i]:
            G.add_edge(i, j)

    color = list(mpl.colors.TABLEAU_COLORS.values())
    node_color = []
    for i in result:
        node_color.append(color[i[1]])
    plt.clf()
    pos = nx.spring_layout(G)
    nx.draw(G, pos, node_color=node_color, font_size= 35,with_labels=True)

结果如下:

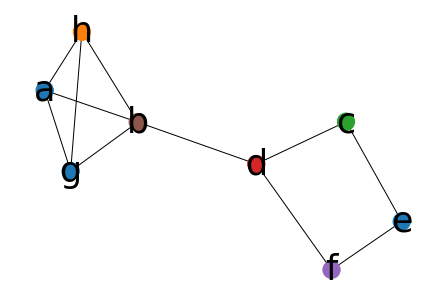
很明显这个不是最优解,把f可以换成棕色，c可以换成橙色，这样就用4种颜色来着色

之所以产生这样的问题，其一是：这个算法本身就是一种贪心策略的算法，难免会掉入局部最优

其次是这个算法的第一步是对顶点进行排序，排序的时候相同度数的顶点的顺序其实是不确定的，也会导致结果不优

图的着色就是这么多了，继续学习下一章吧！