# 图的数据结构 -- 潘登同学的图论笔记
@
节点数据结构
在数据结构中我们可以知道,图由节点和边构成,那么想实现图的数据结构就必然离不开节点Node,为了避免混淆,我的节点同一命名为Vertex;
那么实现Vertex需要一些什么属性和方法呢?
- 节点的名称
- 节点的与什么节点连接以及连接的权值
- 增加相邻节点(或者叫修改相邻节点的边权值)
- 获得相邻节点(就是通过这个节点知道他的相邻节点是什么)
- 获得节点名称(由Vertex对象获得自己的名称)
- 获得相邻边数据(通过相邻的节点的名称知道他们之间的权值)
- 显示设置(如果在命令行把Vertex输入, 显示的东西, 如果不写的话, 就会显示对象地址)
class Vertex:
def __init__(self, key):
self.id = key
self.connectedTo = {} # connectedTo用于储存相邻节点 key是相邻节点(对象而不是名称) value是连接权值
def addNeighbor(self, nbr, weight=0): # 增加相邻边,默认weight为0
'''
input:
nbr: Vertex object
weight: int
return:
None
'''
self.connectedTo[nbr] = weight
def getConnections(self): # 获得相邻节点
'''
input: None
return: Vertex object
'''
return self.connectedTo.keys()
def getId(self): # 获得节点名称
'''
input: None
return: key(str)
'''
return self.id
def getWeight(self, nbr): # 获得相邻边数据
'''
input: Vertex object
return: weight(int)
'''
return self.connectedTo[nbr]
def __str__(self): # 显示设置(__str__是内置方法,也就是不需要显示的使用这个方法就可以用这个函数)
return str(self.id) + 'connectTo:' + \
str([x.id for x in self.connectedTo])
if __name__ == '__main__':
# 与节点相关的数据, 链接表
a_info = {'x1':['y3', 'y5']}
# 新建节点
x1 = Vertex('x1')
y3 = Vertex('y3')
y5 = Vertex('y5')
# 根据邻接表添加相邻节点
x1.addNeighbor(y3, 1)
x1.addNeighbor(y5, 5)
# 测试定义的函数功能
# 获取节点id
print(x1.getId())
print(y5.getId())
# 获取节点的相邻节点
print(x1.getConnections())
print(x1)
# 由相邻节点获得与相邻节点的权值
print(x1.getWeight(y5))
图数据结构
实现完节点了,接下来就是实现图了;
那么图的数据结构都包括什么呢?
- 图的一种储存数据的方式就是邻接表,采取邻接表来储存节点
- 图的节点个数
- 在图中增加节点
- 通过节点的key获得节点对象
- 判断节点在不在图中(in 内置函数)
- 新增两节点的边
- 获取所有节点的名称
- 迭代器的实现(通过for 循环把vertex对象取出)
话不多说 上代码!
import Vertex # 导入上面写的代码
class Graph:
def __init__(self):
self.vertList = {} # 这个虽然叫list但是实质上是字典
self.numVertices = 0 # 记录节点个数
def addVertex(self, key): # 增加节点
'''
input: Vertex key (str)
return: Vertex object
'''
self.numVertices = self.numVertices + 1
newVertex = Vertex(key) # 创建新节点
self.vertList[key] = newVertex
return newVertex
def getVertex(self, key): # 通过key获取节点信息
'''
input: Vertex key (str)
return: Vertex object
'''
if key in self.vertList:
return self.vertList[key]
else:
return None
def __contains__(self, n): # 判断节点在不在图中
'''
input: Vertex key (str)
return: bool
'''
return n in self.vertList
def addEdge(self, from_key, to_key, cost=1): # 新增边
'''
input:
from_key: vertex key (str)
to_key: vertex key (str)
cost: int
return:
None
'''
if from_key not in self.vertList: # 不再图中的顶点先添加
self.addVertex(from_key)
if to_key not in self.vertList:
self.addVertex(to_key)
# 调用起始顶点的方法添加邻边
self.vertList[from_key].addNeighbor(self.vertList[to_key], cost)
def getVertices(self): # 获取所有顶点的名称
return self.vertList.keys()
def __iter__(self): # 迭代取出
return iter(self.vertList.values()) # 采用iter直接转成可迭代对象
def __len__(self): # 查看节点个数
return self.numVertices
if __name__ == '__main__':
# 邻接表
g_dict ={'1':[['2', 10], ['3', 10]],
'2':[['3', 2], ['4', 4], ['5', 8]],
'3':[['5', 9]],
'4':[['6', 10]],
'5':[['4', 6], ['6', 10]]}
# 创建graph对象
g = Graph()
# 在Graph中vertList的数据结构其实就是上面这个
# 遍历g_dict
for from_key in g_dict:
for to_key in g_dict[from_key]:
g.addEdge(from_key, to_key[0], [0, to_key[1]])
# 测试通过节点名称获取节点
print(g.getVertex('3'))
# 获得所有节点的名称
print(g.getVertices())
# 查看节点个数
print(len(g))
# 判断节点在不在图中
print('7' in g, '3' in g)
OK!!, 现在我们已经成功实现了图的数据结构
细心的同学已经注意到了, 上面刚刚出现了邻接表这个词语, 当然总是跟他相提并论的还有邻接矩阵,我们先把这两个概念说清楚;
图的邻接表
图的邻接表存储法。邻接表既适用于存储无向图,也适用于存储有向图;
在具体讲解邻接表存储图的实现方法之前,先普及一个"邻接点"的概念。在图中,如果两个点相互连通,即通过其中一个顶点,可直接找到另一个顶点,则称它们互为邻接点;
邻接指的是图中顶点之间有边或者弧的存在;
例如,存储图 1a) 所示的有向图,其对应的邻接表如图 1b) 所示:

拿顶点 V1 来说,与其相关的邻接点分别为 V2 和 V3,因此存储 V1 的链表中存储的是 V2 和 V3 在数组中的位置下标 1 和 2;
简化起见
我喜欢把邻接表定义为一个字典, 字典的keys储存出发点, values是一个长度为 2 的list, list的第一个元素表示到达点, 第二个元素表示weight
- 具体代码就是这样
# 邻接表
g_dict ={'1':[['2', 10], ['3', 10]],
'2':[['3', 2], ['4', 4], ['5', 8]],
'3':[['5', 9]],
'4':[['6', 10]],
'5':[['4', 6], ['6', 10]]}
'1':[['2', 10], ['3', 10]] 就表示顶点'1'出发到达顶点'2'的权值是10, 到达顶点'3'的权值是10;
图的邻接矩阵
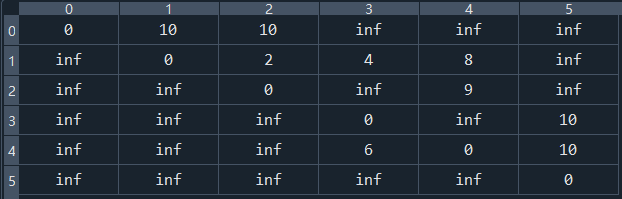
图的邻接矩阵大家都很熟悉, 就是用一个矩阵来表示点与点之间的关系, 沿用上面邻接表的例子;
- 具体长这样
import numpy as np
np.array([[0, 10, 10, np.inf, np.inf, np.inf],
[np.inf, 0, 2, 4, 8, np.inf],
[np.inf, np.inf, 0, np.inf, 9, np.inf],
[np.inf, np.inf, np.inf, 0, np.inf, 10],
[np.inf, np.inf, np.inf, 6, 0, 10],
[np.inf, np.inf, np.inf, np.inf, np.inf, 0]])
 好了!我们已经介绍完图的数据结构了, 那现在我们开始系统的学习图论吧!!
好了!我们已经介绍完图的数据结构了, 那现在我们开始系统的学习图论吧!!

