# 图的匹配 -- 潘登同学的图论笔记
@
- 顶点支配,独立与覆盖 (前提假设,G是没有孤立顶点的简单图)
设$G = (V,E)$是无向简单图, $D⊆V$, 若对于任意 $v∈V-D$,都存在$u∈D$,使得$uv∈E$,则称D为一个支配集
若D是图G的支配集,且D的任何真子集都不再是支配集,则称D为一个极小支配集;
若图G的支配集D满足对于G的任何支配集D'都有|D| ≤ |D'|,则称D为G的一个最小支配集(不唯一)
最小支配集的元素个数称为图G的支配数
(注:极小支配集不一定是最小支配集,但是最小支配集一定是极小支配集)
- 例子1:

{v5,v6,v7}是支配集
{v6,v7}是极小支配集,也是最小支配集
{v3,v6}是极小支配集,也是最小支配集
例子2:
(a)在任一简单图G(V,E)中,V是支配集
(b)完全图Kn(n≥3)的支配数为1
(c)完全二部图Km,n的支配数为min(m,n)
(d)轮图Wn(n≥3)的支配数为1 (因为轮图中有一个点连接所有点)
独立集
设G=(V,E,r)是一个无向图, S⊆V ,若对于任意的u,v∈S, 都有u与v不相邻, 则称S是G的一个点独立集或简称独立集(∅是任意图的独立集)
若对G的任何独立集T,都有S⊄T,则称S是G的一个极大独立集;
具有最大基数的独立集为最大独立集,其中点的个数称为G的独立数
注:(a) 极大点独立集不是任何其他点独立集的子集
(b)若点独立集S是G的一个极大独立集,则对于任意u∈V-S,都存在v∈S,使得u与v相邻
(c)最大独立集,极大独立集 都是不唯一的
(d)最大独立集是极大, 但极大不一定是最大
- 例子: > (a) 完全图Kn(n≥3)的独立数为1 > > (b) 完全二部图Km,n的支配数为max(m,n) > > (c) 圈图Cn(n≥3)的独立数为 floor(n/2)(向下取整) (隔一个取一个) > > (d) 轮图Wn(n≥3)的独立数为 floor(n/2)(向下取整) (隔一个取一个)
独立数和支配数的关系
定理> 一个独立集也是支配集当且仅当他是极大独立集
证明: (充分性)假设S是图的一个极大独立集,他不是支配集,则存在顶点v与S中所有顶点都不相邻,这与S作为独立集的'极大性'相矛盾;
(必要性)如果S是独立集也是支配集,但不是极大独立集,则有独立集S1,满足S⊆S1,考虑顶点u∈S1-S,则u与S中所有顶点都不相邻,这与S是支配集矛盾;
定理> 无向简单图的极大独立集也是极小支配集(反之不然)
证明: (若S是图的极大独立集, 显然是支配集)
下证: 其为极小支配集
(反证法) 若s不是极小支配集,则存在集合S1⊆S,S1也是支配集,考虑顶点u∈S1-S, 则u必与S1中的某顶点相邻,与S是独立集相矛盾;
(反之不然)可以看回上例子1 , {v3,v6}是极小支配集但显然不是独立集
点覆盖 (用点去覆盖边)
设G(V,E)是简单图, V'⊆V, 如果对于任意e∈E,都存在v∈V',使得v是e的一个端点,则称V'是G的一个点覆盖集,简称点覆盖
若V'是图G的点覆盖,且V’的任何真子集都不再是点覆盖,则称V'是一个极小点覆盖
如果图G的点覆盖$V'$满足对于G的任何点覆盖$V''$都有$|V'| ≤ |V''|$,则称V'是G的一个最小覆盖,其V'中元素个数称作覆盖数,记为β(G)
例子:
(a)在任一简单图G(V,E)中,V是点覆盖
(b)完全图Kn(n≥3)的覆盖数为1
(c)完全二部图Km,n的覆盖数为min(m,n)
(d)圈图Cn(n≥3)的覆盖数为 ceiling(n/2)(向上取整)
(e)轮图Wn(n≥3)的覆盖数为 ceiling(n/2) + 1(向上取整)
定理在简单图G(V,E)中, V'⊆V是点覆盖集当且仅当V-V'是独立集
证明:(必要性)假设$V'⊆V$是点覆盖集,若$V-V'$是不独立集,则存在顶点$u,v∈V-V'$,使得$u,v$相邻,而这与$V'$是点覆盖集产生矛盾(因为边uv没有被覆盖)
(充分性)如果$V-V’$是独立集, 但$V'⊆V$不是点覆盖集, 则存在边$uv∈E$, 使得$u,v ∉ V'$,于是$u,v∈V-V’$;而$u,v$相邻与$V-V’$是独立集相矛盾;
妙蛙妙蛙!!!!
前面的铺垫都差不多了,接下来进入正题了
匹配
设G=(V,E)是简单图, M⊆E, 如果M中任何两条边都不邻接,则称M为G的一个匹配或边独立集
设顶点v∈V,若存在e∈M,使得v是e的一端点,则称v是
M-饱和的,否则称v是M-非饱和的
最大匹配数
若匹配M满足对任意e∈E-M,M∪{e,}(这个逗号是显示问题) 不再构成匹配,则称M是G的一个极大匹配(不唯一)
如果图G的匹配M满足对于G的任何匹配M都有$|M|≥|M’|$,则称M是G的一个最大基数匹配或最大匹配 或
最大匹配,最大匹配的元素个数称为图G的匹配数(记为V(G))完全匹配 (把所有顶点都用上)
饱和图中每个顶点的匹配称作完全匹配或完全匹配
注:(a) 在完美匹配中,每个顶点都关联匹配中的一条边;
(b)如果图G存在完美匹配,则图G的匹配数为G的阶数的一半,此时的阶数为偶数(不一定所有图都有完美匹配)
(c)每个完美匹配都是最大匹配,但最大匹配不一定是完美匹配
- 例子: > (a) 完全图Kn(n≥3)的匹配数为 floor(n/2) > > (b) 完全二部图Km,n的匹配数为min(m,n) > > (c) 圈图Cn(n≥3)的匹配数为 floor(n/2)(向下取整) > > (d) 轮图Wn(n≥3)的匹配数为 ceiling(n/2)(向上取整)
构成最大匹配的充要条件
- 交错道路 > 设M是G中一个匹配, 若G中一条初级道路是由M中的边和E-M中的边交替出现组成的,则称其为交错道路
一条交错道路如下图,绿色的一个匹配,从B1一直到A5的一条红绿相间的道路就是交错道路

可增广道路
若一条交错道路的始点和终点都是非饱和点,则称其为M-可增广道路 (注:可增广道路的长度是奇数)
伯奇引理匹配M为图G = (V,E)的最大匹配当且仅当G中不存在M-可增广道路
证明:(必要性)假设M是最大匹配,且存在一条M-可增广道路$e_1,e_2,...,e_{2k+1}$,则$e_2,e_4,...,e_{2k}$为属于M的边$e_1,e_2,...,e_{2k+1}$为不属于M的边;
构造新集合$M1 =(M-{e_2,e_4,...,e_{2k}})∪{e_1,e_2,...,e_{2k+1}}$; 易证M1也是G的一个匹配。但$|M1| = |M| + 1$,与M为最大匹配相矛盾
(也可以之间看特殊情况:${e_1, e_3, ..., e_{2k+1}}$构成的匹配数就是|M|+1)
(充分性)如果G中不存在M-可增广道路,而M不是最大匹配,则必有最大匹配M1;
令M2 = M1 ∪ M, 则(新构造)图(V,M2)中所有顶点度数不超过2, 因此图(V,M2)中每个连通分支要么是一个单独的回路(要么是一个单独的道路)而且道路是交错的
由于|M1|>|M|, 因此M2中原本属于M1的边多余原本属于M的边。所以一定存在一条交错道路以M1的边开始.以M1的边结束,于是它就是一条M-可增广道路;
邻接顶点集
设W是图G的顶点集的一个子集,则Ng(w) = {v|存在u∈w, 使得u与v相邻}称作W的邻接顶点集
(算法)最大匹配算法 MaxMatch(G)
输出:二部图 G = (X,Y,E)
输出: G的一个最大匹配M
① 任选一个初始匹配,给饱和顶点标记为1,其余为0
② while X中存在0:
- 2.1 选择一个0标记点x∈X, 令u←{x}, v←∅
- 2.2 若Ng(u) = v, 则x无法作为一条增广道路的端点,给x标记为2, 转②
- 2.3 否则,选择y∈Ng(u) - v
- 2.31 若y的标记为1,则存在边yz∈M,令u←u∪{z}, v←v∪{y},转 2.2
- 2.32 否则,存在一条x至y的可增广道路P,令M←M∪P,给x和y标记1, 转②
(注:算法中标记1表示已饱和的顶点, 0表示未处理的顶点)
在写算法之前当然还要处理一下数据结构,对Vertex节点对象新增labels属性,在增加修改labels的方法和获取labels的方法
再重写一个二部图的数据结构Bin_Graph,与Graph的主要区别就是把节点分别储存到两个字典中了,所以整个数据结构要重写,不过万变不离其宗
话不多说,上代码!!!
#%%最大匹配
from Vertex import Vertex # 导入Vertex
class New_Vertex(Vertex):
def __init__(self,key):
super().__init__(key)
self.labels = 0 # 新增类属性(节点标记)
# 新增类方法 设置标记
def setlabel(self, label):
self.labels = label
# 新增类方法 获得标记值
def getlabel(self):
return self.labels
class Bin_Graph():
# 这里因为要划分X与Y的点集,所以重写一个图的数据解构,与原本的Graph区别也不太大
def __init__(self):
self.x_vertList = {} # 储存x的顶点
self.y_vertList = {} # 储存y的顶点
self.numVertices = 0
def addVertex(self, key, label): # 增加节点
self.numVertices = self.numVertices + 1
newVertex = New_Vertex(key) # 创建新节点
if label == 'x':
self.x_vertList[key] = newVertex
elif label == 'y':
self.y_vertList[key] = newVertex
return newVertex
def getVertex(self, key): # 通过key获取节点信息
if key in self.x_vertList:
return self.x_vertList[key]
elif key in self.y_vertList:
return self.y_vertList[key]
else:
return None
def __contains__(self, n): # 判断节点在不在图中
return n in self.x_vertList or n in self.y_vertList
def addEdge(self, from_key, to_key, label, cost=1): # 新增边
if (from_key not in self.x_vertList) and (from_key not in self.y_vertList):
return print('from_key不在图中!!')
if (to_key not in self.x_vertList) and (to_key not in self.y_vertList):
return print('to_key不在图中!!')
# 调用起始顶点的方法添加邻边
if label == 'x':
self.x_vertList[from_key].addNeighbor(self.y_vertList[to_key], cost)
elif label == 'y':
self.y_vertList[from_key].addNeighbor(self.x_vertList[to_key], cost)
def addUndirectedEdge(self, key1, key2, cost=1):
self.addEdge(key1, key2, 'x', cost)
self.addEdge(key2, key1, 'y', cost=1)
def get_x_Vertices(self): # 获取所有x顶点的名称
return self.x_vertList.keys()
def get_y_Vertices(self): # 获取所有y顶点
return self.y_vertList.keys()
def __iter__(self): # 迭代取出
return iter(list(self.x_vertList.values()) + list(self.y_vertList.values()))
def __len__(self):
return self.numVertices
class Solution(): # 解决具体问题的类对象
# 创建二部图
def createBinpartiteGraph(self, a_dict):
'''
Parameters
----------
a_dict : dict对象,keys用于存放X,Values用于存放Y
Returns
-------
bin_Graph : Bin_Graph二部图对象
'''
bin_Graph = Bin_Graph()
for i in a_dict:
bin_Graph.addVertex(i, 'x')
for j in a_dict[i]:
# 如果y不在图中就先添加
if j not in bin_Graph.get_y_Vertices():
bin_Graph.addVertex(j, 'y')
bin_Graph.addUndirectedEdge(i, j)
return bin_Graph
# 求出邻接顶点集
def Ng(self, w, g):
'''
w:图g的一个顶点集的子集, 其中元素表示的是节点的名称
return: w的邻接顶点集, 其中的元素表示的是节点的名称
'''
neighbors = []
for i in w:
temp = list(g.getVertex(i).getConnections())
neighbors += [i.getId() for i in temp]
return neighbors
# 算法实现(最大匹配)
def MaxMatch(self, g):
'''
g: 二部图
return: 最大匹配m 字典,keys表示y values表示x
'''
m = {}
# 如果x的顶点里面有0标记的
while (0 in [g.getVertex(i).getlabel() for i in g.get_x_Vertices()]):
# 选择一个标记为0的x
for x in g.get_x_Vertices():
if g.getVertex(x).getlabel() == 0:
# U中装的是节点的keys
U = [x]
V = []
neibor = self.Ng(U, g)
while True: # 这里设置while循环因为下面要回来这里
turn130while = False
# 如果Ng(U, g)=V, 则x无法作为一条可增广道路的端点,将x标记为2
if neibor == V:
# 将x标记为2
g.getVertex(U[0]).setlabel(2)
# 退回到130行while
turn130while = True
break
else:
turn130while = False
# 选择y属于neibor - V
diff = [i for i in neibor if i not in V]
for y in diff:
if g.getVertex(y).getlabel() == 1:
# 修改U,V
if m[y] not in U:
U.append(m[y])
if y not in V:
V.append(y)
# 退回到138行while循环
break
else:
turn130while = True
# 把x,y加到可增广道路
m[y] = x
# 修改x,y的标记
g.getVertex(x).setlabel(1)
g.getVertex(y).setlabel(1)
# 退回到130while循环 需要两步
break
if turn130while:
break
if turn130while:
break
return m
if __name__ == '__main__':
a_dict = {'x1':['y3', 'y5'],
'x2':['y1', 'y2', 'y3'],
'x3':['y4'],
'x4':['y4', 'y5'],
'x5':['y5']}
s = Solution()
g = s.createBinpartiteGraph(a_dict)
print(s.MaxMatch(g))
结果输出了 {'y3': 'x1', 'y1': 'x2', 'y4': 'x3', 'y5': 'x4'},这就是一个最大匹配,在下图(就是本题的二部图)中找不到更大的匹配比找到的这个匹配多;

霍尔定理> 设$G=(X,Y,E)$为二部图,G中存在使X中每个顶点饱和的匹配M(即|M|=|X|) 当且仅当对任何非空集合$S⊆X,|N_g(s)|≥|S|$ (该条件表示任意子集都有足够多的相邻顶点)
证明: (必要性)假定存在匹配M⊆E使得X中每个顶点饱和,则$|N_g(S)|≥|N_{(X,Y,M)}(S)| = |s|$ ((X,Y,M)表示二部图G)
(充分性)假设M是一个最大匹配,且存在M-非饱和顶点x∈X;
① 如果x是孤立顶点,则$|N_g({x})| = 0 < 1 = |{x}|$, 与条件矛盾
② 否则,考虑所有从x开始的交错道路,记Y中所有x可以通过这些道路到达的顶点为集合T,记X中所有x可以通过这些道路到达的顶点为集合W, 由于所有从x开始的极长的(不能再延长)交错道路的终点都不能是Y中M-非饱和顶点(否则将产生M-可增广道路,与M是最大匹配矛盾)所以T中顶点都是M-饱和顶点。
记R为从x开始的所有交错道路的边形成的集合,则R∩M中的边构成了W-{x}和T中顶点一 一对应,$|W-{x}| = |T|$
下证: $N_g(W) = T$
(反证法) 存在$y∈N_g(W)-T$,则 存在$z∈W$,使得$zy∈E$, 又因为$W-{x}$和T中元素都是M-饱和点或X本身,因此$zy ∉ M$
于是,要么x就是z;要么x可以通过某条交错道路到达z,再经过边zy可以到达y; 这都与$y ∉ T$矛盾;
最后,$|w| = |W-{x}| + 1 > |W-{x}| = |T| = |N_g(W)|$ 与 条件($|N_g(s)|≥|S|$)相矛盾 (证毕)
(虽然上面说了这么唬人的一大堆,但是这个定理想说明白的事情很简单,就是现在由一堆男的和一堆女的进行约会的匹配, 想要让男的都能有约会对象的充要条件就是男的认识足够多的女的,如:一个男的至少认识一个女的(或者更多))
推论> 设$G = (X,Y,E)$为二部图,若存在正整数K,使得对任意x∈X,由$deg(x)≥k$,对任意$y∈Y$, 由$deg(x) ≤ k$,则G中存在使X中每个饱和点的匹配.
证明: 假设非空集合S⊆X,则S中顶点关联的边至少K|S|条,而这些边都与Ng(S)中的顶点相关联,由于Y中顶点度数都不超过K,因此$|N_g(S)|≥ \frac{K|S|}{K} = |S|$ .所以存在使X中每个顶点饱和的匹配
推论> 对任意正整数k,k-正则二部图中必定存在使X中每个顶点饱和的匹配
直观例子(以2-正则二部图为例)

拉丁方
霍尔定理的应用
- 称每行每列都包含给定的n个符号恰一次的n阶方阵为拉丁方
例子:集合{1,2,3,4}的4阶拉丁方 $$ L1 = \begin{bmatrix} 1 & 2 & 3 & 4\ 2 & 3 & 4 & 1\ 3 & 4 & 1 & 2\ 4 & 1 & 2 & 3\ \end{bmatrix} L2 = \begin{bmatrix} 1 & 2 & 3 & 4\ 3 & 4 & 1 & 2\ 4 & 3 & 2 & 1\ 2 & 1 & 4 & 3\ \end{bmatrix} $$
(算法)构造拉丁方(书上讲得很繁琐)我设计一个算法就是先随机构建一个序列,然后后面的每一行都是把整个序列向右移动一位就好比L1
边覆盖
- 边覆盖(用边去覆盖点) > 设G=(V,E)是没有孤立顶点的简单图, $E'⊆E$,如果对任意的$v∈V$,都存在$e∈E’$,使得v是e的一个端点,则称$E'$为G的一个边覆盖 > > E'的任何真子集都不是边覆盖,则称为极小边覆盖 > > 如果图G的边覆盖$E'$满足对于任何边覆盖$E''$,都有$|E’| ≤|E''|$,则称$E'$是G的一个最小边覆盖,其元素个数称作覆盖数,记作P(G)
注: (a)有孤立顶点的简单图不存在边覆盖
(b)极小边覆盖E’中任何一条边的两个端点不可能都与E'中的其他边关联
(c)明显有$P(G) ≥ \frac{|V|}{2}$
(d)一个图中的极小边覆盖,最小边覆盖都不唯一
(e)最小边覆盖是极小,但极小不一定是最小
- 例子: > (a)在任一简单图G(V,E)中,E都是边覆盖 > > (b)任何完美匹配都是最小边覆盖 > > (c)完全图Kn(n≥3)的边覆盖数为 ceiling(n/2) > > (d)完全二部图Km,n的支配数为max(m,n) > > (e)圈图Cn(n≥3)的边覆盖数为 ceiling(n/2) > > (f)轮图Wn(n≥3)的边覆盖数为 floor(n/2) + 1
最大匹配与最小边覆盖之间的关系
- 定理1
设G=(V,E)是没有孤立顶点的简单图,M为G的一个匹配,N为G的一个边覆盖,则$|N| ≥ P(G)(最小边覆盖数) ≥ |V|/2 ≥ V(G)(最大匹配数) ≥ |M|$; 且当等号成立时,M为G的一个完美匹配,N为G的一个最小边覆盖
(这个定理很显然,就不证啦)
- 定理2
设G=(V,E)是没有孤立顶点的简单图,则有
(a)设M为G的一个最大匹配,对G中每一个M-非饱和顶点均取一条与其关联的边,组成集合N,则M∪N构成G的一个最小边覆盖,
图示如下:

(b)设N为G的一个最小边覆盖,若N存在相邻的边,则移去其中一条,直至不存在相邻的边为止,构成的边集合M则为G的一个最大匹配
图示如下:
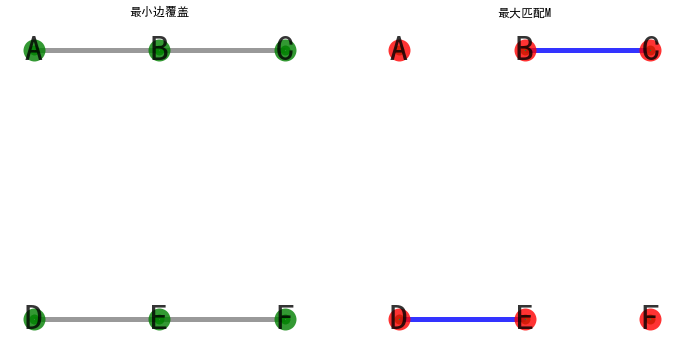
(c) P(G) + V(G) = |V|
(三条一起证)证明:
(a)由于M为G的一个最大匹配,因此G由$n-2 * V(G)$个非饱和顶点,不可能有两个相邻的非饱和顶点,因此$|N| = n-2 * V(G),|M∪N| = n-2 * V(G) + V(G) = n-V(G)$ 显然M∩N构成了G中的一个边覆盖,因此$n-V(G)≥P(G)$
(b)由于N是一个最小边覆盖,因此N中任何一条边的两个端点不可能都与其他边相关联。所以从N中移去边的时候,产生且只产生了M中的一个M-非饱和顶点。而最终M-非饱和顶点的个数 为$n-2|M|$, 故移去边的数目是$n-2|M|$(因为移去一个边就产生一个非饱和点)。得到$|M| = |N| - (n-2|M|) \geq |N| = n - |M|$; 又因为|N|是最小边覆盖:$P(G)= |N| = n - |M| ≥ n - V(G)$(因为$V(G)(最大匹配数) ≥ |M|$)
(c)由(a)可得$n-V(G)≥P(G)$;由(b)可得$P(G) ≥ n - V(G)$; 所以$P(G) = n - V(G)$;即$P(G) + V(G) = |V|$
柯尼希给出:二部图中匹配数和最小点覆盖数的相等关系
- 引理 > 假设K为没有孤立顶点的简单图G的任意一个点覆盖集,M为G的任意一个匹配,则$|M|≤|K|$。 特别是$V(G) ≤ β(G)$(点覆盖数,用点去覆盖边)
证明: 因为一个顶点覆盖一条边, 而对于一个匹配,只需要与匹配数相同的点就能实现点覆盖, 那么剩余的每一个非饱和点都用一个点去覆盖;所以$V(G) ≤ β(G)$
推论> 假设K为没有孤立顶点的简单图G的任意一个点覆盖集,M为G的任意一个匹配, 若|M| = |K|, 则M是一个最大匹配,K是一个最小覆盖
证明: 由$|M| ≤ V(G)≤ β(G)≤ |K|$即得 (第一个等号成立条件:最大匹配;第二个等号成立条件:引理:第三个等号成立条件:最小覆盖)
柯尼希-艾盖尔瓦里定理> 二部图中最大匹配的匹配数 = 最小点覆盖的覆盖数
证明:
假设M为最大匹配,V'为G的一个最小点覆盖集
(1) 由上面引理$|M| ≤ |V'|$
(2) 令$X_c = V'∩X, Y_d = V'∩Y, C = |X_c|, d = |Y_d|$
考虑顶点为$X_c∪(Y-Y_d)$的G的导出子图G’,它也是二部图,其中存在使$X_c$中每个顶点饱和的匹配M1;
(反证法) 若存在$S⊆X_c$, $|N_{G'}(S)|<|S|$ ($N_{G'}(S)$表示G'中与S相邻的点)
则$(V'-S)∪N_{G'}(S)$同样构成了点覆盖集,但元素小于$V'$, 与$V'$的最小性矛盾
同理,顶点为$(X-X_c)∪Y_d$的G的导出子图$G'$, 它也是二部图,其中存在使$Y_d$中每个顶点饱和的匹配M2
易见$M1∪M2$也是G的一个匹配,于是$|M| ≥ |M1∪M2| = |M1| + |M2| = |X_c| + |Y_d| = |V'|$
再结合(1),可得$|M| = |V'|$
由最大匹配构造最小点覆盖
①如果X中不存在M-非饱和顶点,则X本身就是一个最小点覆盖集
(如果x是孤立顶点,则不会出现在任何匹配和最小点覆盖中,因此不考虑所有孤立顶点)
②X中存在M-非饱和顶点, 考察所有从x开始的交错道路,记Y中所有x可以通过这些道路到达的顶点为集合$Y_x$,并记$Y_1 = Yx ∪(x∈X)$
易见每个$Y_1$中的元素都与M中唯一的一条边关联,记M中与$Y_1$中的元素关联的边集合为M1,则$|Y_1| = |M1|$,记X中与M-M1相关联的顶点集合为$X_1$,则$|X_1| = |M| - |M1|$; 明显有$|Y_1∪X_1| = |Y_1| + |X_1| = |M|$
断言: Y1∪X1就是一个最小点覆盖
只需证明:$Y_1∪X_1$是一个点覆盖集即可,('最小性'由最大匹配数决定)
(反证法)如果存在边$uv,u∈X-X_1,v∈Y-Y_1,则由X_1,Y_1$的构造方法可知:
或者u本身是M-非饱和点,经过uv可到达顶点v; 或者存在M-非饱和顶点x∈X,以x开始的某一条交错道路P可到达顶点u;这两者都能与$v∈Y-Y_1$相矛盾;
二部图的匹配
(算法)最大权匹配(指派问题)
输入:赋权完全二部图 G = (X,Y,E)
输出: G的一个最大权匹配
在这里我主要用DFS来遍历所有组合然后选出最大的权匹配即可
- 具体题目描述 n个人干n项工作,第i个人干第j项工作能获得Cij单位收益, 要求把人跟工作匹配,收益总和最大
C = [[12,7,9,7,9],[8,9,6,6,6],[7,17,12,14,12],[15,14,6,6,10],[4,10,7,10,6]]
#%%最大权匹配(指派问题)
import copy
def template(matrix): # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
result = [] # 这个保存结果
profit = 1e10
def trace(path, choices): # 递归函数
'''
path: dict 用于储存找到的零 key表示row values表示column
choices: 矩阵matrix
'''
nonlocal result,profit
if len(path) == len(matrix): # 当path的长度等于输入的n时,结束算法,把结果加入结果列表
# 计算profit
temp = 0
for row in path:
temp += choices[row][path[row]]
# 比较当前方案与此前最优方案
if temp < profit:
result = copy.deepcopy(path)
profit = temp
return
for row in range(len(choices)):
for column in range(len(choices)):
if row in path.keys():
continue
if column in path.values(): # 减枝操作(如果path里面有column,说名这一列已经有零了)
continue
path[row] = column # 如果没有就把他加到目前的path中
trace(path, choices) # 递归调用自身
path.popitem() # 撤销最后一次的选择继续向前找答案
trace({}, matrix) # 调用函数trace
return result
if __name__ == '__main__':
C = [[12,7,9,7,9],
[8,9,6,6,6],
[7,17,12,14,12],
[15,14,6,6,10],
[4,10,7,10,6]]
print(template(C))
可以看到结果输出的是{0: 2, 1: 4, 2: 1, 3: 0, 4: 3},带回C矩阵中发现,确实是最大的,再次说明了DFS是很有效且用途很广泛的算法
既然由最大权匹配当然也有最小权匹配
(算法)最小权匹配(指派问题)
输入:赋权完全二部图 G = (X,Y,E)
输出: G的一个最小权匹配
- 具体题目描述 n个人干n项工作,第i个人干第j项工作能消耗Cij单位时间, 要求把人跟工作匹配,时间耗费最小
C = [[12,7,9,7,9],[8,9,6,6,6],[7,17,12,14,12],[15,14,6,6,10],[4,10,7,10,6]]
#%%最小权匹配(指派问题)
def template(matrix): # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
result = [] # 这个保存结果
profit = 1e10
def trace(path, choices): # 递归函数
'''
path: dict 用于储存找到的零 key表示row values表示column
choices: 矩阵matrix
'''
nonlocal result,profit
if len(path) == len(matrix): # 当path的长度等于输入的n时,结束算法,把结果加入结果列表
# 计算profit
temp = 0
for row in path:
temp += choices[row][path[row]]
# 比较当前方案与此前最优方案
if temp < profit:
result = copy.deepcopy(path)
profit = temp
return
for row in range(len(choices)):
for column in range(len(choices)):
if row in path.keys():
continue
if column in path.values(): # 减枝操作(如果path里面有column,说名这一列已经有零了)
continue
path[row] = column # 如果没有就把他加到目前的path中
trace(path, choices) # 递归调用自身
path.popitem() # 撤销最后一次的选择继续向前找答案
trace({}, matrix) # 调用函数trace
return result
if __name__ == '__main__':
C = [[12,7,9,7,9],
[8,9,6,6,6],
[7,17,12,14,12],
[15,14,6,6,10],
[4,10,7,10,6]]
print(template(C))
可以看到结果输出的是{0: 1, 1: 2, 2: 0, 3: 3, 4: 4},带回C矩阵中发现,确实是最小的
细心的同学可能看出来了上面这个结果好像跟之前矩阵找零的那个结果一样,对的这两题用的矩阵都是同一个矩阵,只不过找零的那题的矩阵是用了Hungary算法处理过的
图的匹配就是这么多了,继续学习下一章吧!

