# Canopy聚类、层次聚类、密度聚类-DBSCAN -- 潘登同学的Machine Learning笔记
书接上文说完了K-means, 接着说说其他的聚类方法
Canopy聚类
Canopy聚类算法是一个将对象分组到类的简单、快速、精确地方法。每个对象用多维特征空间里的一个点来表示。这个算法使用一个快速近似距离度量和两个距离阈值$T_1>T_2$来处理。
注意Canopy聚类很少单独使用, 一般是作为k-means前不知道要指定k为何值的时候,用Canopy聚类来判断k的取值
(算法)步骤
输入:所有点的集合D, 超参数:$T_1,T_2, 且T_1>T_2$
输出:聚类好的集合
- 1.随机选择一个节点做canopy的中心C;并从D删除该点;
- 2.遍历D: 计算其到各个canopy中心的距离;
- 2.1如果该点到中心C的距离小于$T_2$,那么给该点打上强标记,从D中删除该点
- 2.2如果该点到中心C的距离小于$T_1$,那么给该点打上弱标记(但是它们并不会从D中被移除,也就是说,它们将会参与到下一轮的聚类过程中,成为新的canopy类的中心或者成员)
- 2.3如果到任何中心C的距离都大于$T_1$,那么将这个点作为一个新的canopy的中心,并从list中删除这个元素;
- 3.如果D非空,再来一遍; 否则结束算法
注意
- 当T1过大时,会使许多点属于多个Canopy,可能会造成各个簇的中心点间距离较近,各簇间区别不明显;
- 当T2过大时,增加强标记数据点的数量,会减少簇个个数;
- T2过小,会增加簇的个数,同时增加计算时间;
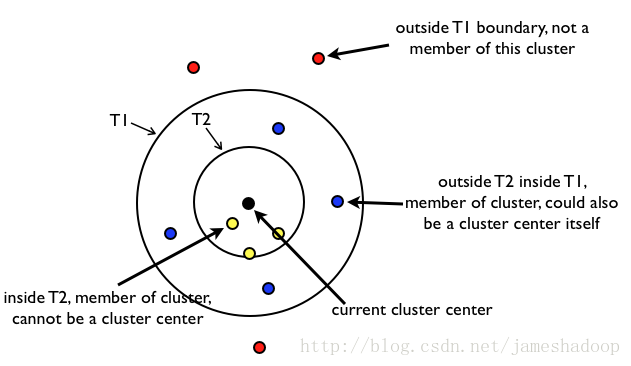
一幅图说明算法:
内圈的一定属于该类, 外圈的一定不属于该类, 中间层的可能属于别的类(因为不止一个聚类中心, 他可能属于别的类的内圈);
上代码!!!
对iris数据集做Canopy聚类, 半径分别设置为1和2
#%% Canopy聚类
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import copy
class Solution(object):
def Canopy(self, x, t1, t2):
'''
Parameters
----------
x : array
数据集.
t1 : float
外圈半径.
t2 : float
内圈半径.
Returns
-------
result: list.
聚好类的数据集
'''
if t1 < t2:
return print("t1 应该大于 t2")
x = copy.deepcopy(x)
result = [] # 用于存放最终结果
index = np.zeros((len(x),)) # 用于标记外圈外的点 1表示强标记, 2表示弱标记
while (index == np.zeros((len(x),))).any():
alist = [] # 用于存放某一类的数据集
choice_index = None
for i, j in enumerate(index):
if j == 0:
choice_index = i
break
C = copy.deepcopy(x[choice_index])
alist.append(C)
x[choice_index] = np.zeros((1, len(x[0])))
index[choice_index] = 1
for i,a in enumerate(x):
if index[i] != 1:
distant = (((a-C)**2).sum())**(1/2)
if distant <= t2: # 打上强标记
alist.append(copy.deepcopy(x[i]))
x[i] = np.zeros((1, len(x[0])))
index[i] = 1
elif distant <= t1:
index[i] = 2
result.append(alist)
return result
def pint(r, x, y, c):
# 点的横坐标为a
a = np.arange(x-r,x+r,0.0001)
# 点的纵坐标为b
b = np.sqrt(np.power(r,2)-np.power((a-x),2))
plt.plot(a,y+b,color=c,linestyle='-')
plt.plot(a,y-b,color=c,linestyle='-')
plt.scatter(x, y, c='r',marker='*')
if __name__ == '__main__':
data = pd.read_csv(r'C:/Users/潘登/Documents/python全系列/人工智能/iris.csv')
X = np.array(data.iloc[:, 2:4])
Y = data['species']
result = Solution().Canopy(X, 2, 1)
x1 = []
y1 = []
for i in result[0]:
x1.append(i[0])
y1.append(i[1])
x2 = []
y2 = []
for i in result[1]:
x2.append(i[0])
y2.append(i[1])
x3 = []
y3 = []
for i in result[2]:
x3.append(i[0])
y3.append(i[1])
plt.figure(figsize=(16,12))
plt.scatter(X[:,0], X[:,1], s=50, c='violet', marker='s')
plt.scatter(x1, y1, s=50, c='orange', marker='s')
plt.scatter(x2, y2, s=50, c='lightblue', marker='s')
plt.scatter(x3, y3, s=50, c='blue', marker='s')
pint(2, x1[0], y1[0], 'b')
pint(1, x1[0], y1[0], 'y')
pint(2, x2[0], y2[0], 'b')
pint(1, x2[0], y2[0], 'y')
pint(2, x3[0], y3[0], 'b')
pint(1, x3[0], y3[0], 'y')
plt.xlim([0, 8])
plt.ylim([-3, 5])
plt.show()
+结果如下:

层次聚类
解决了k-means k值选择和初始中心点选择的问题
分裂法
- (算法)步骤 输入:所有点的集合D
输出:聚类好的集合
- 1.将所有样本归为一个簇
- 2.当不足k个簇(或者距离阈值)时,否则结束算法
- 2.1在同一个簇中计算样本间的距离, 选择最远的距离的两个样本a,b
- 2.2将样本a,b划入$C_1, C_2$
- 2.3计算原簇中样本离谁近, 划入谁
- 3.返回2
凝聚法
- (算法)步骤 输入:所有点的集合D
输出:聚类好的集合
- 1.将每个样本看成一个独立的簇
- 2.当多于k个簇(或者距离阈值)时,否则结束算法
- 2.1在两两簇之间计算簇间的距离, 选择最近距离的簇$C_1, C_2$
- 2.2合并$C_1, C_2$
- 3.返回2
合并$C_1, C_2$的方式
两个簇之间距离的度量
- 两个簇间距离最小的样本的距离
- 两个簇间距离最远的样本的距离
- 两个簇间两两求距离的平均值
- 两个簇间两两求距离的中位数
- 求每个集合的中心点, 用中心点的距离代表簇的距离
上代码
# %%层次聚类
import numpy as np
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram
from sklearn.datasets import load_iris
from sklearn.cluster import AgglomerativeClustering
def plot_dendrogram(model, **kwargs):
# 创建连杆矩阵,然后绘制树状图
# 创建每个节点下的样本计数
counts = np.zeros(model.children_.shape[0])
n_samples = len(model.labels_)
for i, merge in enumerate(model.children_):
current_count = 0
for child_idx in merge:
if child_idx < n_samples:
current_count += 1 # leaf node
else:
current_count += counts[child_idx - n_samples]
counts[i] = current_count
linkage_matrix = np.column_stack(
[model.children_, model.distances_, counts]
).astype(float)
# 绘制相应的树状图
dendrogram(linkage_matrix, **kwargs)
if __name__ == '__main__':
iris = load_iris()
X = iris.data
# 设置distance_threshold=0确保我们计算的是完整的树。
model = AgglomerativeClustering(distance_threshold=0, n_clusters=None)
model = model.fit(X)
plt.title("Hierarchical Clustering Dendrogram")
# 绘制树状图的最上面四层
plot_dendrogram(model, truncate_mode="level", p=4)
plt.xlabel("Number of points in node (or index of point if no parenthesis).")
plt.show()
- 结果如下:
由于空间问题就只展现最上面4层的簇合并情况

密度聚类-DBSCAN
一个基于密度聚类的算法 ,与层次聚类不同 它将簇定义为密度相连的点的最大集合,能够把具有高密度的区域划分为簇,并可有效地对抗噪声
先引入几个概念
- $\varepsilon$领域: 以一个点为圆心, 半径为$\varepsilon$的圆形成的空间
- 核心对象: 给定数目m, 如果某个点(对象)的$\varepsilon$领域内, 至少含有m个点(对象), 该对象就是核心对象
- 直接密度可达: 给定一个对象集合D, 如果p在q的e领域内,而q是一个核心对象, p从q出发是直接密度可达的
密度可达: 密度可达是在直接密度可达的基础上的, 如果存在一个对象链$p_1,p_2,\ldots,p_n$. 令$p_1=p,p_n=q$, $p_{i+1} 从 p_i$出发关于$\varepsilon、m$是直接密度可达的, 那么p和q就是关于$\varepsilon、m$密度可达
密度相连: 密度相连是在密度可达的基础之上的, 如果集合D中存在一个对象o 使o->p 密度可达,o->q密度可达,那么p和q就是关于$\varepsilon、m$密度相连
下图直观地展现了这几个概念

DBSCAN算法的核心思想是:用一个点的$\varepsilon$邻域内的邻居点数衡量该点所在空间的密度,该算法可以找出形状不规则的cluster,而且聚类的时候事先不需要给定cluster的数量。
(算法)步骤
输入:所有点的集合D, $\varepsilon、m$
输出:聚类好的集合
- 1.如果一个点x的ε邻域包含多余m个对象,则创建一个x作为核心对象的新簇;
- 2.寻找并合并核心对象直接密度可达的对象;
- 3.没有新点可以更新簇的时候,算法结束。
算法特征描述:
- 1、每个簇至少包含一个核心对象。
- 2、非核心对象可以是簇的一部分,构成簇的边缘。
- 3、包含过少对象的簇被认为是噪声。
上代码
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
def expand(a, b):
d = (b - a) * 0.1
return a-d, b+d
if __name__ == "__main__":
N = 1000
centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)
data = StandardScaler().fit_transform(data)
# 数据的参数:(epsilon, min_sample)
params = ((0.2, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12, 8), facecolor='w')
plt.suptitle(u'DBSCAN聚类', fontsize=20)
for i in range(6):
eps, min_samples = params[i]
model = DBSCAN(eps=eps, min_samples=min_samples)
model.fit(data)
y_hat = model.labels_
core_indices = np.zeros_like(y_hat, dtype=bool)
core_indices[model.core_sample_indices_] = True
y_unique = np.unique(y_hat)
n_clusters = y_unique.size - (1 if -1 in y_hat else 0)
print(y_unique, '聚类簇的个数为:', n_clusters)
plt.subplot(2, 3, i+1)
clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size))
print(clrs)
for k, clr in zip(y_unique, clrs):
cur = (y_hat == k)
if k == -1:
plt.scatter(data[cur, 0], data[cur, 1], s=20, c='k')
continue
plt.scatter(data[cur, 0], data[cur, 1], s=30, c=clr, edgecolors='k')
plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], s=60, c=clr, marker='o', edgecolors='k')
x1_min, x2_min = np.min(data, axis=0)
x1_max, x2_max = np.max(data, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.title(u'epsilon = %.1f m = %d,聚类数目:%d' % (eps, min_samples, n_clusters), fontsize=16)
plt.tight_layout()
plt.subplots_adjust(top=0.9)
plt.show()
- 结果如下:

Canopy聚类、层次聚类、密度聚类-DBSCAN就是这样了, 继续下一章吧! pd的Machine Learning