密度最大值聚类、谱聚类

作者: pdnbplus | 发布时间: 2024/07/13 | 阅读量: 55

# 密度最大值聚类、谱聚类 -- 潘登同学的Machine Learning笔记

密度最大值聚类

密度最大值聚类是一种简洁优美的聚类算法, 可以识别各种形状的类簇, 并且参数很容易确定。

  • 局部密度：
    ρi=∑jχ(dij−dc),其中χ(x)={1,x<00,otherwise\rho_i = \sum_{j}\chi(d_{ij} - d_c), 其中 \chi(x)= \begin{cases} 1, x<0\\ 0, otherwise \end{cases}

dcd_c是一个截断距离， ρi\rho_i是所有点中到ii的距离小于dcd_c的点的个数，即ρi=\rho_i =任何一个点以dcd_c为半径的圆内的样本点的数量

dcd_c的设定经验， 使平均每个点的邻居数目是所有点的1%-2%;

  • 高局部密度点距离：
    δi=minj:ρj>ρi(dij)\delta_i = min_{j:\rho_j>\rho_i}(d_{ij})

δi\delta_i表示在密度高于ii的对象中的所有对象中, 离ii最近的点到ii的距离

特别地， 对于密度最大的对象， 设置高局部密度距离为max⁡dij\max d_{ij}

簇中心和异常点的识别

依据上面的概念定义， 我们可以选取蔟中心的判断异常点了

ρ大δ大 --- 簇中心

ρ小δ大 ---- 异常值

解释：

  • ρ\rho大说明周围的点很多
  • δ\delta大说明另一个密度大的离我很远（换句话说，就是我是方圆几里内最大的那个）
  • 那么蔟中心肯定得是ρ大δ大， 异常值则是ρ小δ大
  • 那么对于ρ大δ小的点，就说明他的周围点也很多， 但是周围的点中有比他大的， 所以他就属于某一类（但不是中心）
  • 那么对于ρ小δ小的点， 只能说这个点是某一类的边缘点， 因为旁边有比他密度大的点

举个栗子

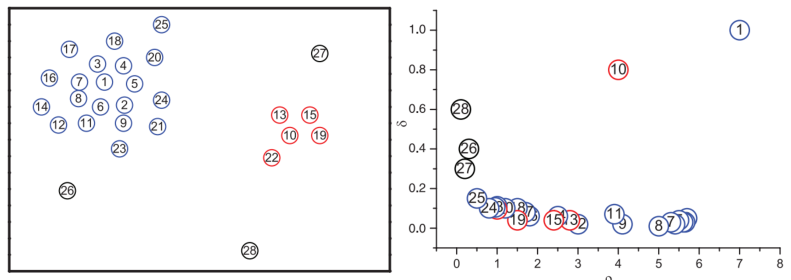
簇中心和异常点的识别

上图中， 横轴为ρ\rho, 纵轴为δ\delta

先看ρ大δ大的点， 那不就是1和10，他俩就是簇中心；

再看ρ小δ大的点， 那不就是26、27、28， 他们就是异常值；

再看ρ小δ小的点， 那不就是25、24， 他们就是蓝色类别的边缘点；

谱聚类

以下内容来自刘建平Pinard-博客园的学习笔记， 有些许补充及修改

谱聚类分为构图和切图两个步骤

概念引入

邻接矩阵

对于无向图G(V,E)， 定义矩阵中的元素wijw_{ij}, 表示点ViV_i到VjV_j的距离

由于是无向图， wij=wjiw_{ij} = w_{ji}
W=[w11w12⋯w1nw21w22⋯w2n⋮⋮⋱⋮wn1wn2⋯wnn]W = \begin{bmatrix} w_{11} & w_{12} & \cdots & w_{1n} \\ w_{21} & w_{22} & \cdots & w_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n1} & w_{n2} & \cdots & w_{nn} \\ \end{bmatrix}

度矩阵

对于图中的任意一个点viv_i,它的度did_i和它相连的所有边的权重之和
di=∑j=1nwijd_i = \sum_{j=1}^nw_{ij}
根据定义， 度矩阵D是一个n×nn\times n的对角阵
D=[d1d2⋱dn]D = \begin{bmatrix} d_{1} & & & \\ & d_{2} & & \\ & & \ddots & \\ & & & d_{n} \\ \end{bmatrix}

相似矩阵

由于数据间的点间没有权重， 所以需要我们自己定义；

由相似矩阵构造邻接矩阵的基本思想是： 距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，不过这仅仅是定性，我们需要定量的权重值。一般来说，我们可以通过样本点距离度量的相似矩阵S来获得邻接矩阵W。

构建邻接矩阵W的方法有三类。ε\varepsilon-邻近法，K邻近法和全连接法。

  • ε\varepsilon-邻近法

它设置了一个距离阈值ε\varepsilon，然后用欧式距离xijx_{ij}度量任意两点xix_{i}和xjx_{j}的距离。即相似矩阵的sij=∣∣xi−xj∣∣22s_{ij}=||x_i−x_j||_2^2, 然后根据sijs_{ij}和ε\varepsilon的大小关系，来定义邻接矩阵W如下：
wij={0,sij>εε,sij<εw_{ij} = \begin{cases} 0, s_{ij} > \varepsilon\\ \varepsilon, s_{ij} < \varepsilon\\ \end{cases}

从上式可见，两点间的权重要不就是ε\varepsilon,要不就是0，没有其他的信息了。距离远近度量很不精确，因此在实际应用中，我们很少使用ε\varepsilon-邻近法。

  • K邻近法

利用KNN算法遍历所有的样本点，取每个样本最近的k个点作为近邻，只有和样本距离最近的k个点之间的wij>0。但是这种方法会造成重构之后的邻接矩阵W非对称，我们后面的算法需要对称邻接矩阵。为了解决这种问题，一般采取下面两种方法之一：

第一种K邻近法是只要一个点在另一个点的K近邻中，则保留sij=e−∣∣xi−xj∣∣222σ2s_{ij}=e^{-\frac{||x_i−x_j||_2^2}{2\sigma^2}}
wij=wji={0xi∉KNN(xj)and  xj∉KNN(xi)sijxi∈KNN(xj)or  xj∈KNN(xi)w_{ij} = w_{ji} = \begin{cases} 0 &{x_i \notin KNN(x_j) and \; x_j \notin KNN(x_i)}\\ s_{ij} &{x_i \in KNN(x_j) or \; x_j \in KNN(x_i)}\\ \end{cases}

第二种K邻近法是必须两个点互为K近邻中，才能保留sijs_{ij}
wij=wji={0xi∉KNN(xj)or  xj∉KNN(xi)sijxi∈KNN(xj)and  xj∈KNN(xi)w_{ij} = w_{ji} = \begin{cases} 0 &{x_i \notin KNN(x_j) or \; x_j \notin KNN(x_i)}\\ s_{ij} &{x_i \in KNN(x_j) and \; x_j \in KNN(x_i)}\\ \end{cases}

  • 全连接法

第三种方法所有的点之间的权重值都大于0，因此称之为全连接法。可以选择不同的核函数来定义边权重，常用的有多项式核函数，高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF，此时相似矩阵和邻接矩阵相同：
wij=sij=e−∣∣xi−xj∣∣222σ2w_{ij} = s_{ij} = e^{-\frac{||x_i−x_j||_2^2}{2\sigma^2}}

拉普拉斯矩阵

拉普拉斯矩阵要根据前面的两个矩阵来构造
L=D−WL = D - W

而拉普拉斯矩阵具有如下性质：

  • 拉普拉斯矩阵是对称矩阵，这可以由D和W都是对称矩阵而得
  • 由于拉普拉斯矩阵是对称矩阵，则它的所有的特征值都是实数
  • 对于任意的向量α\alpha,有
    αTLα=12∑i,j=1nwij(αi−αj)2\alpha^TL\alpha = \frac{1}{2}\sum_{i,j=1}^{n}w_{ij}(\alpha_i-\alpha_j)^2
  • 拉普拉斯矩阵是半正定的，且对应的n个实数特征值都大于等于0

推导
αTLα=αTDα−αTWα=∑i=1ndiαi2−∑i,j=1nwijαiαj=12(∑i=1ndiαi2−∑i,j=1nwijαiαj+∑j=1ndjαj2)=12∑i,j=1nwij(αi−αj)2\begin{aligned} \alpha^TL\alpha &= \alpha^TD\alpha - \alpha^TW\alpha\\ &= \sum_{i=1}^nd_i\alpha_i^2-\sum_{i,j=1}^nw_{ij}\alpha_i\alpha_j\\ &= \frac{1}{2}(\sum_{i=1}^nd_i\alpha_i^2-\sum_{i,j=1}^nw_{ij}\alpha_i\alpha_j+\sum_{j=1}^nd_j\alpha_j^2)\\ &= \frac{1}{2}\sum_{i,j=1}^{n}w_{ij}(\alpha_i-\alpha_j)^2 \end{aligned}

无向图切图

对于无向图G的切图，我们的目标是将图G(V,E)切成相互没有连接的k个子图，每个子图点的集合为：A1,A2,…AkA_1,A_2,\ldots A_k，它们满足Ai∩Aj=∅A_i\cap A_j=\empty,且A1∪A2∪…∪Ak=VA_1\cup A_2\cup \ldots \cup A_k=V.

  • 对于任意两个子图点的集合A,B⊂VA,B\subset V, A∩B=∅A\cap B=\empty, 我们定义A和B之间的切图权重为：
    W(A,B)=∑i∈A,j∈BwijW(A,B)=\sum_{i\in A,j \in B}w_{ij}

  • 那么对于我们k个子图点的集合：A1,A2,…AkA_1,A_2,\ldots A_k，我们定义切图cut为：
    cut(A1,A2,...Ak)=12∑i=1kW(Ai,Aiˉ)cut(A1,A2,...Ak)=\frac{1}{2}\sum_{i=1}^kW(A_i, \bar{A_i})
    其中Aiˉ\bar{A_i}为AiA_i的补集，意为除AiA_i子集外其他V的子集的并集。

我们的总目标：让子图内的点权重和高，子图间的点权重和低

两种切图方式

RatioCut切图

RatioCut(A1,A2,…,Ak)=12∑i=1kW(Ai,Aiˉ)∣Ai∣RatioCut(A_1, A_2, \ldots, A_k) = \frac{1}{2}\sum_{i=1}^k\frac{W(A_i, \bar{A_i})}{|A_i|}

其中，∣Ai∣|A_i|就是子集A中点的个数， 要想子图内的点权重和高，子图间的点权重和低， 那么就只需要最小化上面的函数

引入引入指示向量hj∈{h1,h2,…,kk},j=1,2,…,kh_j \in \{h_1, h_2, \ldots, k_k\},j=1,2,\ldots,k,对于任意一个向量hjh_j, 它是一个n维向量（n为样本数）
hij={0vi∉Aj1∣Ai∣vi∈Ajh_{ij} = \begin{cases} 0 &{v_i \notin A_j}\\ \frac{1}{\sqrt{|A_i|}} &{v_i \in A_j}\\ \end{cases}

文字表达出来就是： 如果点viv_i不在子图AjA_j中，hijh_{ij}就为0， 否则就是子图中权重和的倒数再开根

注意 hjh_j是一个列向量， 用于刻画所有点与某一个子图的某种关系； H不是方阵， 是一个n×kn\times k的长方形矩阵

对于某个hah_a,有
haTLha=12∑m=1∑n=1wmn(ham−han)2=12(∑m∈Aa,n∉Aawmn(1∣Aa∣−0)2+∑m∉Aa,n∈Aawmn(0−1∣Aa∣)2)=12(∑m∈Aa,n∉Aawmn1∣Aa∣+∑m∉Aa,n∈Aawmn1∣Aa∣)=12(cut(Aa,Aaˉ)1∣Aa∣+cut(Aaˉ,Aa)1∣Aa∣)=cut(Aa,Aaˉ)∣Aa∣\begin{aligned} h_a^TLh_a &= \frac{1}{2}\sum_{m=1}\sum_{n=1}w_{mn}(h_{am}-h_{an})^2\\ &= \frac{1}{2}(\sum_{m\in A_a,n \notin A_a}w_{mn}(\frac{1}{\sqrt{|A_a|}}-0)^2 + \sum_{m\notin A_a,n \in A_a}w_{mn}(0-\frac{1}{\sqrt{|A_a|}})^2)\\ &= \frac{1}{2}(\sum_{m\in A_a,n \notin A_a}w_{mn}\frac{1}{|A_a|} + \sum_{m\notin A_a,n \in A_a}w_{mn}\frac{1}{|A_a|})\\ &= \frac{1}{2}(cut(A_a, \bar{A_a})\frac{1}{|A_a|} + cut(\bar{A_a},A_a)\frac{1}{|A_a|})\\ &= \frac{cut(A_a,\bar{A_a})}{|A_a|} \end{aligned}

喔！！ 这不就是我们要最小化的函数吗！！
RatioCut(A1,A2,…,Ak)=∑i=1kW(Ai,Aiˉ)∣Ai∣=∑i=1khiTLhi=∑i=1k(HTLH)ii=tr(HTLH)\begin{aligned} RatioCut(A_1, A_2, \ldots, A_k) &= \sum_{i=1}^k\frac{W(A_i, \bar{A_i})}{|A_i|}\\ &= \sum_{i=1}^kh_i^TLh_i\\ &= \sum_{i=1}^k(H^TLH)_{ii}\\ &= tr(H^TLH)\\ \end{aligned}

所以我们的切图目标为：
arg min⁡Htr(HTLH)s.t.HTH=1(因为特征向量是单位化的)\argmin_H tr(H^TLH)\\ s.t. H^TH = 1(因为特征向量是单位化的)

这里与我们之前讲的PCA很相似， 但是有不同的地方, 之前PCA是从数据的协方差矩阵中选择前面几个大的特征值对应的属性作为降维后的特征；

注意:
而这里就是从拉普拉斯矩阵的特征值矩阵中抽取几个小的特征值，作为切图的依据， 因为H矩阵是一个n×kn\times k的长方形矩阵， 可以理解为， 只选择了特征值小的对应的特征向量组成了H矩阵， 所以这个特征值矩阵HTLHH^TLH就是k×kk\times k的

通过找到L的最小的k个特征值，可以得到对应的k个特征向量，这k个特征向量组成一个nxk维度的矩阵，即为我们的H。一般需要对H矩阵按行做标准化，即
hij∗=hij(∑t=1khit2)12h_{ij}^* = \frac{h_ij}{(\sum_{t=1}^k h_{it}^2)^{\frac{1}{2}}}

最后，由于我们在使用维度规约的时候损失了少量信息，导致得到的优化后的指示向量h对应的H现在不能完全指示各样本的归属，因此一般在得到nxk维度的矩阵H后还需要对每一行进行一次传统的聚类，比如使用K-Means聚类.

Ncut切图

Ncut切图和RatioCut切图很类似，但是把Ratiocut的分母∣Ai∣|A_i|换成vol(Ai)vol(A_i)(子图内的点权重和). 由于子图样本的个数多并不一定权重就大，我们切图时基于权重也更合我们的目标，因此一般来说Ncut切图优于RatioCut切图。
NCut(A1,A2,…,Ak)=12∑i=1kW(Ai,Aiˉ)vol(Ai)NCut(A_1, A_2, \ldots, A_k) = \frac{1}{2}\sum_{i=1}^k\frac{W(A_i, \bar{A_i})}{vol(A_i)}

对应的, Ncut切图对指示向量h做了改进
hij={0vi∉Aj1vol(Ai)vi∈Ajh_{ij} = \begin{cases} 0 &{v_i \notin A_j}\\ \frac{1}{\sqrt{vol(A_i)}} &{v_i \in A_j}\\ \end{cases}

对于某个hah_a,有
αTLα=cut(Aa,Aaˉ)vol(Aa)\alpha^TL\alpha = \frac{cut(A_a,\bar{A_a})}{vol(A_a)}

推导方式和RatioCut完全一致。也就是说，我们的优化目标仍然是
NCut(A1,A2,…,Ak)=tr(HTLH)NCut(A_1, A_2, \ldots, A_k) = tr(H^TLH)

但是此时我们的HTH≠IH^TH≠I,而是HTDH=IH^TDH=I。

推导如下：
hiTDhi=∑j=1nhij2dj=1vol(Ai)∑j∈Aidj=1vol(Ai)vol(Ai)=1h_i^TDh_i = \sum_{j=1}^nh_{ij}^2d_j = \frac{1}{vol(A_i)}\sum_{j\in A_i}d_j = \frac{1}{vol(A_i)}vol(A_i) = 1

此时我们的H中的指示向量h并不是标准正交基，所以在RatioCut里面的降维思想不能直接用。

转化一下

我们令H=D−12FH=D^{-\frac{1}{2}}F, 则：HTLH=(FTD−12)L(D−12F)，HTDH=FTF=IH^TLH=(F^TD^{-\frac{1}{2}})L(D^{-\frac{1}{2}}F)，H^TDH=F^TF=I,也就是说优化目标变成了:
arg min⁡F=(FTD−12)L(D−12F)s.t.FTF=I\argmin_F = (F^TD^{-\frac{1}{2}})L(D^{-\frac{1}{2}}F)\\ s.t. F^TF = I
可以发现这个式子和RatioCut基本一致，只是中间的L变成了D−12LD−12D^{-\frac{1}{2}}LD^{-\frac{1}{2}}。这样我们就可以继续按照RatioCut的思想，求出D−12LD−12D^{-\frac{1}{2}}LD^{-\frac{1}{2}}的最小的前k个特征值，然后求出对应的特征向量，并标准化，得到最后的特征矩阵F,最后对F进行一次传统的聚类（比如K-Means）即可。

一般来说， D−12LD−12D^{-\frac{1}{2}}LD^{-\frac{1}{2}}相当于对拉普拉斯矩阵L做了一次标准化，即
L∗=Lijdi∗djL^* = \frac{L_{ij}}{\sqrt{d_i*d_j}}

（算法）谱聚类算法流程

最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式，最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。下面以Ncut总结谱聚类算法流程。

输入：样本集D=(x1,x2,...,xn)D=(x_1,x_2,...,x_n)，相似矩阵的生成方式, 降维后的维度k1k_1, 聚类方法，聚类后的维度k2k_2

输出： 簇划分C(c1,c2,...ck2)C(c_1,c_2,...c_{k2}).

  • 根据输入的相似矩阵的生成方式构建样本的相似矩阵S
  • 根据相似矩阵S构建邻接矩阵W，构建度矩阵D
  • 计算出拉普拉斯矩阵L=D−WL = D - W
  • 构建标准化后的拉普拉斯矩阵D−12LD−12D^{-\frac{1}{2}}LD^{-\frac{1}{2}}
  • 计算D−12LD−12D^{-\frac{1}{2}}LD^{-\frac{1}{2}}最小的k1k_1个特征值所各自对应的特征向量f
  • 将各自对应的特征向量f组成的矩阵按行标准化，最终组成n×k1n\times k_1维的特征矩阵F
  • 对F中的每一行作为一个k1k_1维的样本，共n个样本，用输入的聚类方法进行聚类，聚类维数为k2k_2
  • 得到簇划分C(c1,c2,...ck2)C(c_1,c_2,...c_{k2}).

谱聚类算法总结

  • 谱聚类算法的主要优点有：
    • 谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
    • 由于使用了降维，因此在处理高维数据聚类时的复杂度比传统聚类算法好。
  • 谱聚类算法的主要缺点有：
    • 如果最终聚类的维度非常高，则由于降维的幅度不够，谱聚类的运行速度和最后的聚类效果均不好。
    • 聚类效果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能很不同。

密度最大值聚类、谱聚类就是这样了， 继续下一章吧！ pd的Machine Learning