多元线性回归(MLR) -- 潘登同学的Machine Learning笔记
总目标:预测模型:$$ y = \beta_0 + \beta_1x_1 + \cdots + \beta_kx_k $$优化目标:预测的越精确越好, 预测误差(残差)越小越好Actual value:真实的y值(样本中自带的)
Predicted value:预测的y值(通过多元线性回归得出的y,通常记作 $\hat{y}$
error:预测值与真实值的误差(error = $\hat{y} - y$)
loss:表示我们最优化的目标,我们希望残差越小越好
$$ Loss = \sum_{n=1}^{m} error^{2} = \sum_{n=1}^{m} (\hat{y} - y)^{2} $$
求解目标:$$ \min_{\beta_0,\beta_0,\ldots,\beta_k} Loss = \min_{\beta_0,\beta_0,\ldots,\beta_k} \sum_{n=1}^{m} error^{2} = \min_{\beta_0,\beta_0,\ldots,\beta_k} \sum_{n=1}^{m} (\hat{y} - y)^{2} $$ 上述目标称为MSE(Mean Square Error),我们习惯用$\theta$来代替这一串${\beta_0,\beta_0,\ldots,\beta_k}$
由极大似然估计(MLE, Maximum likelihood estimation)推导MSE
- 理解为什么$\theta$不是唯一的 > 因为数据都是从总体中抽样出来的,只要我们的样本不同,${\theta}$就不会相同,我们将特定样本计算出的${\theta}$称为$\hat{\theta}$,所以我们只能得到$\hat{\theta}$的无偏估计,而不能得到${\theta}$的无偏估计(除非我们的样本就是总体);
问题1: 那么我们凭什么能用样本计算出的$\hat{\theta}$来代替${\theta}$
- 解决上面的问题, 采用中心极限定理

问题2: 中心极限定理又跟$\hat{\theta}$可以当作${\theta}$有什么关系呢?
- 构造似然函数,最大化总似然
假若说我们已经对样本进行了模型求解,那么我们得到了某个具体的$\hat{\theta_1}$
那么这个$\hat{\theta_1}$到底有多像${\theta}$呢?
给定一个概率分布 D,已知其概率密度函数(连续分布)或概率质量函数(离散分布)为 f_D,以及一个分布参数θ,我们可以从这个分布中抽出一个具有 m 个值的采样 $x_1,x_2,\ldots,x_m$,利用f_D计算似然函数: $$ L(\theta|x_1,x_2,\ldots,x_m) = f_{\theta}(x_1,x_2,\ldots,x_m)$$
若 D 是离散分布,$f_{\theta}$ 即是在参数为θ时观测到这一采样的概率。若其是连续分布,$f_{\theta}$ 则为 $x_1,x_2,\ldots,x_m$ 联合分布的概率密度函数在观测值处的取值。
一旦我们获得了$x_1,x_2,\ldots,x_m$,那么我们就能获得一个关于${\theta}$的估计(也就是$\hat{\theta}$)
最大似然估计会寻找关于${\theta}$的最可能的值(即在所有可能 的${\theta}$取值中,寻找一个值使这个采样的“可能性”最大化)。从数学上来说,我们可以在${\theta}$的所有可能取值中寻找一个值使得
似然函数取到最大值。这个使可能性最大的$\hat{\theta}$值即称为${\theta}$的最大似然估计。由定义,最大似然估计是关于样本的函数。
问题3:那这个概率密度函数是什么呢?
由中心极限定理,这个概率密度函数是正态分布,其概率密度函数为 $$ f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$
但是我们需要的是估计${\theta}$, 我们转变一下思路,只要在给定样本$X_{m\times n}$,计算出$\hat{\theta}$之后, 其实$\hat{y}$就知道了, 那么误差项 $\varepsilon$就能知道了, 且$\varepsilon$的大小其实跟$\hat{\theta}$准不准确是有极大关联的(很好理解,$\hat{\theta}$越准确,$\varepsilon$越小, 这个可以证明);
所以我们可以用$\varepsilon$来做最大似然估计 $$ f(\varepsilon_i|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\varepsilon_i-\mu)^2}{2\sigma^2}} $$
而$\varepsilon$的均值为0, 这个其实是我们的一项假设, 但是它其实也不是假设, 当我们完成我们的优化目标时, 这个均值假设其实就变成一个可以推导出的结论;所以上式改写成: $$ f(\varepsilon_i|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\varepsilon_i-0)^2}{2\sigma^2}} $$
那么我们的似然函数就可以表示为: $$ L_\theta(\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_m)=f(\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_m|\mu,\sigma^2) $$
又因为残差$\varepsilon$服从正态分布, 自然暗含了相互独立的假设,可以把上面的式子写成连乘的形式: $$ f(\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_m|\mu,\sigma^2)=f(\varepsilon_1|\mu,\sigma^2)f(\varepsilon_2|\mu,\sigma^2)\cdots*f(\varepsilon_m|\mu,\sigma^2) $$ 进而有: $$ L_\theta(\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_m) = \prod_{i=1}^{m} f(\varepsilon_i|\mu,\sigma^2) = \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\varepsilon_i-0)^2}{2\sigma^2}} $$
把$x_i$和$y_i$带入上式:
$$
\varepsilon_i = \hat{y} - y = \theta x_i - y_i\
L_\theta(\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_m) = \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\theta ^{T}x_i - y_i)^2}{2\sigma^2}}
$$
最大化总似然:
$$
\argmax_{\theta} L_\theta(\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_m) = \argmax_{\theta} \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\theta ^{T}x_i - y_i)^2}{2\sigma^2}}
$$
- 对数似然函数
对上面总似然函数取对数,得到的函数记为为${\Bbb{L}}$: $$ {\Bbb{L}} = \argmax_{\theta} log_e(\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\theta ^{T}x_i - y_i)^2}{2\sigma^2}})=\argmax_{\theta} \sum_{i=1}^{m}\log_e(\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\theta ^{T}x_i - y_i)^2}{2\sigma^2}}) $$
- 继续往下推(这里省略了,因为只是体力活而已) $$ {\Bbb{L}} = \argmax_{\theta} m\bullet \ln \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{1}{\sigma^2}\bullet\frac{1}{2}\bullet \sum_{i=1}^{m}(\theta ^{T}x_i - y_i)^2 $$ 那么前面一项是常数, 最大化${\Bbb{L}}$就是最小化$\sum_{i=1}^{m}(\theta ^{T}x_i - y_i)^2$
那么,就推导出了我们的优化目标: 残差平方和最小
在Machine Learning中都是通过最小化Loss来达到训练的目的, 所以这个残差平方和就是Loss,并把它称之为MSE;
简单导数知识推导解析解($\theta = (X^TX)^{-1}X^TY$)
$$ \begin{aligned} Loss &= \sum_{i=1}^{m}(\theta ^{T}x_i - y_i)^2 \ &= \sum_{i=1}^{m}(\theta ^{T}x_i - y_i)^{T}\bullet(\theta ^{T}x_i - y_i) \end{aligned} $$
- 借用矩阵运算, 来表示上式
数据矩阵X,Y, 以及待求解的$\theta$ $$ \begin{array}{ccc} \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1n}\ x_{21} & x_{22} & \cdots & x_{2n}\ \vdots & \vdots & \ddots & \vdots\ x_{m1} & x_{m2} & \cdots & x_{mn} \ \end{bmatrix} & \begin{bmatrix} y_{1}\ y_{2}\ \vdots\ y_{m}\ \end{bmatrix} & \begin{bmatrix} \theta_{1}\ \theta_{2}\ \vdots\ \theta_{m}\ \end{bmatrix} \end{array} $$
$$ \begin{aligned} Loss &= (X\theta - Y)^{T}(X\theta - Y)\ &= ((X\theta)^{T} - Y^{T})(X\theta - Y) \ &= (\theta^{T}X^{T} - Y^{T})(X\theta - Y) \ &= (\theta^{T}X^{T}X\theta - \theta^{T}X^{T}Y - Y^{T}X\theta - Y^{T}Y) \ \end{aligned} $$
- 对Loss求导, 得到解析解(矩阵求导法则在这里)
$$ \begin{aligned} Loss' &= ((\theta^{T}X^{T}X\theta)' - (\theta^{T}X^{T}Y)' - (Y^{T}X\theta)' - (Y^{T}Y)') \ &= (2X^{T}X\theta - X^{T}Y - (Y^{T}X)^{T}) \ &= 2(X^{T}X\theta - X^{T}Y) \ &= 0 \end{aligned} $$ 稍微矩阵运算一下, 得到解析解: $$ \theta = (X^TX)^{-1}X^TY $$
来个例子试一试吧
- 一个自变量的情形
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(2)
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
sns.set()
sns.regplot(x, y)
plt.show()
#为了求解w0的截距项,我们给x矩阵左边加上一列全为1的x0
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
w = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)
print(w) #依次为w0 w1...
#绘图查看
x_plot = np.array([[0,2]]).T
x_plot_b = np.concatenate((np.ones((2,1)),x_plot),axis = 1)
y_plot = x_plot_b.dot(w)
plt.plot(x_plot,y_plot,'r-')
plt.plot(x,y,'b.')
plt.show()
- 多个自变量的情形
#%% 多元线性回归
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(2)
x1 = 2*np.random.rand(100,1)
np.random.seed(3)
x2 = 3*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x1 + 3*x2 + np.random.randn(100,1)
#为了求解w0的截距项,我们给x矩阵左边加上一列全为1的x0
x_b = np.concatenate((np.ones((100,1)),x1,x2),axis = 1)
w = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)
print(w) #依次为w0 w1...
#绘图查看
x_plot = np.array([[0,2],
[0,3]]).T
x_plot_b = np.concatenate((np.ones((2,1)),x_plot),axis = 1)
y_plot = x_plot_b.dot(w)
不用解析解, 用梯度下降求解$\theta$
矩阵运算的求解速度还是慢了, 一个m*n的矩阵自己乘自己的转置就要O(m*n),就别说还有求逆操作了, 最主要后面涉及L1、L2正则项加上去之后,解析解就显得很愚蠢了;
梯度下降法> 算法思路:很计算机的算法, 就是看上去很简单但是很有效的方法, 我们想一下我们求解解析解的时候是找导数为0时的$\theta$, 所以关键是找到导数为零的点; > > 梯度下降就是通过不断向负梯度方向前进,就能找到导数为零的点;
如下面这两幅图, 沿着导数的负方向就能找到最小值:
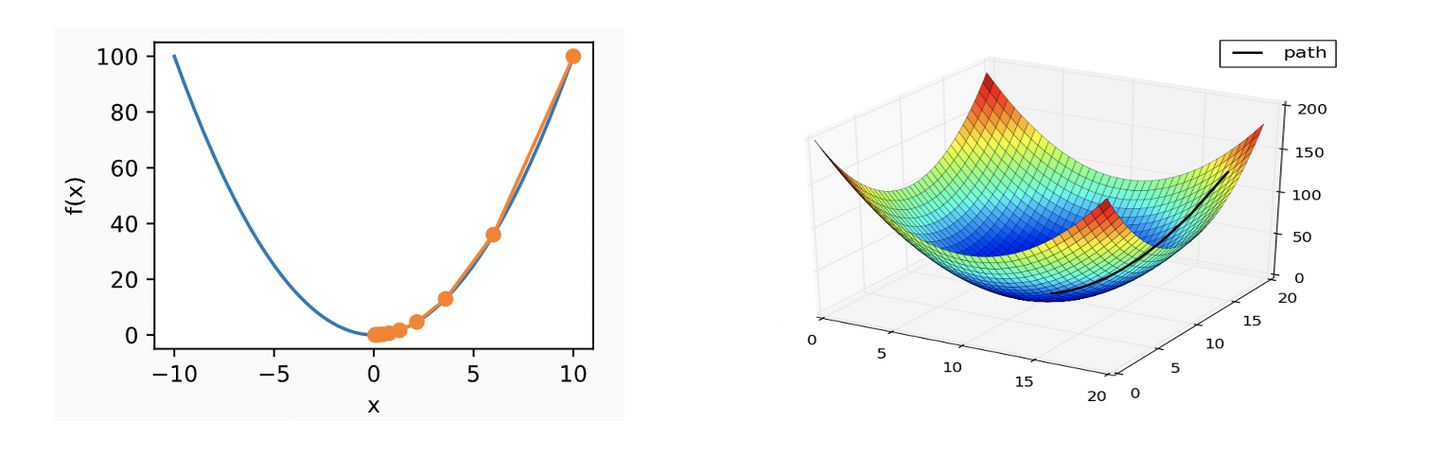
- 一个问题: > 怎么能确定我们找到的这个点就是最小值而不是极小值呢?
有可能是下面这种情况吗?(会落到蓝色点上吗?)
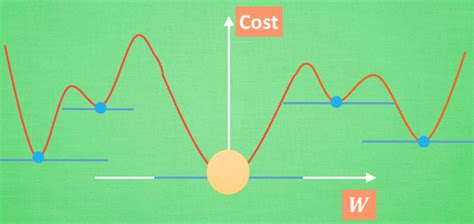
如果单是从算法角度, 确实会进到蓝色点上, 但是Loss函数不长这样,Loss函数是凸函数,就是像上上图这样的只有一个最小值的函数, 很好证明Loss是凸函数:
- 凸函数 > 对区间[a,b]上定义的函数 $f(x)$ ,若它对区间中任意两点$x_1,x_2$均有 $\frac {f(x_1 + x_2)}{2} \leq \frac{f(x1) + f(x2)}{2}$则称 $f(x)$ 为区间[a,b]上的凸函数
然后我们对任意的$x_1,x_2$, 带进Loss, 就用基本不等式很好验证他是凸函数;但是这个方法不够'智能',我们要解放自己的草稿纸!
- Hessian矩阵 > Loss的Hessian阵是对Loss求解二阶导之后得到的矩阵, 要是他的每一个元素都非负, 那么就能说明Loss是凸函数;(因为未知数是$\theta$, 因为我们把他写成了矩阵形式, 实际上他有n个,求了二阶导之后, Hessian阵就是n×n的矩阵)
$$ Hessian= \begin{bmatrix} {\frac{\partial^2{Loss}}{\partial^2{\theta_1}}} & {\frac{\partial^2{Loss}}{\partial{\theta_1}\partial{\theta_2}}} & \cdots & {\frac{\partial^2{Loss}}{\partial{\theta_1}\partial{\theta_n}}}\ {\frac{\partial^2{Loss}}{\partial{\theta_2}\partial{\theta_1}}} & {\frac{\partial^2{Loss}}{\partial^2{\theta_2}}} & \cdots & {\frac{\partial^2{Loss}}{\partial{\theta_2}\partial{\theta_n}}}\ \vdots & \vdots & \ddots & \vdots\ {\frac{\partial^2{Loss}}{\partial{\theta_n}\partial{\theta_1}}} & {\frac{\partial^2{Loss}}{\partial{\theta_n}\partial{\theta_2}}} & \cdots & {\frac{\partial^2{Loss}}{\partial^2{\theta_n}}}\ \end{bmatrix} $$
- 以Hessian阵的第一项为例$\frac{\partial^2 Loss}{\partial^2 \theta_1}$:
(我们要改写一下Loss的表达, 给他前面加个$\frac12$, 只是方便求导) $$ Loss = {\frac{1}{2}(\theta ^{T}{X} - Y)^2} $$
$$ \begin{aligned} \frac{\partial Loss}{\partial \theta_1} & = {\frac{1}{2} \bullet 2(\theta^{T} {X} - Y) \bullet \frac{\partial}{\partial \theta_1}(\theta^{T}X - Y)} \ & = (\theta^{T}X - Y) \bullet {\frac{\partial}{\partial \theta_1}(\sum_{i=0}^{m}\theta_i x_i - y_i)}\ & = (\theta^{T}X - Y)x_1 \ \end{aligned} $$
$$ {\frac{\partial^2 Loss}{\partial^2 \theta_1}} = x_i^2 \geq 0 $$
梯度下降法
$$ \theta_j^{t+1} = \theta_j^{t} - \eta \bullet gradient_j $$
其中$gradient_j$表示$\theta_j$在$\theta_j^{t}$时的梯度(导数);
$\eta$是学习率, 学习率越大,梯度下降的时候迈的步子就越大;
梯度下降示意图:
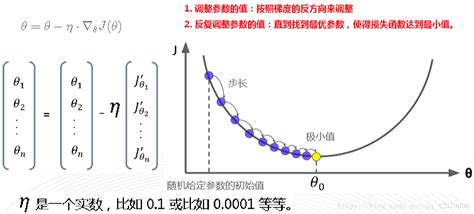
两个关键问题:
问题1: $\theta_j^{1}$是多少?
是多少没所谓, 计算机随机, 爱是多少是多少, 反正随着负梯度方向总能走到最低点
问题2: $\eta$是多少?
学习率的设置是一门学问, 因为设小了他就走的慢, 算法收敛速度就慢; 设置大了, 就可能在最低点的时候跨过最低点, 在最小值附近震荡;一般设置为0.1, 0.01, 0.001, 0.0001这样的数值;
一个在最小值附近震荡例子:
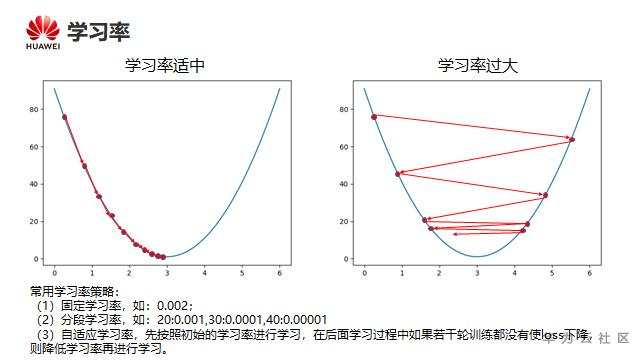
学习率设置对Loss收敛的影响:

(算法)梯度下降法Random 随机$\theta$,随机一组数值 $\theta_0, \theta_1, \ldots, \theta_n$
求梯度gradient
$\theta_j^{t+1} = \theta_j^{t} - \eta \bullet gradient_j$
判断是否收敛 convergence,如果收敛跳出迭代,如果没有达到收敛,回第 2 步继续
$gradient_j$的推导 直接借用之前推凸函数的中间过程 $$ \frac{\partial Loss}{\partial \theta_j} = (\theta^{T}X - Y)x_j $$
那我们就可以得到$gradient_j$: $$ \begin{alignedat}{3} g_0 & = (\theta^{T}X - Y)x_0 \ g_1 & = (\theta^{T}X - Y)x_1 \ g_j & = (\theta^{T}X - Y)x_j \ g_n & = (\theta^{T}X - Y)x_n \ \end{alignedat} $$
(注意)$x_j$表示的是m个样本的属性j的值(是一个m的列向量),可以用矩阵运算检查
另外三种梯度下降法

全量梯度下降(Batch Gradient Descent)
在梯度下降中,对于θ的更新,所有的样本都有贡献,也就是参与调整θ。其计算得到的是一个标准梯度。因而理论上来说一次更新的幅度是比较大的。如果样本不多的情况下, 当然是这样收敛的速度会更快啦。全量梯度下降每次学习都使用整个训练集,因此其优点在于每次更新都会朝着正确的方向进行,最后能够保证收敛于极值点(凸函数收敛于全局极值点,非凸函数可能会收敛于局部极值点),但是其缺点在于每次学习时间过长,并且如果训练集很大以至于需要消耗大量的内存,并且全量梯度下降不能进行在线模型参数更新;
随机梯度下降(Stochastic Gradient Descent)
梯度下降算法每次从训练集中随机选择一个样本来进行学习。批量梯度下降算法每次都会使用全部训练样本,因此这些计算是冗余的,因为每次都使用完全相同的样本集。而随机梯度下降算法每次只随机选择一个样本来更新模型参数,因此每次的学习是非常快速的,并且可以进行在线更新。随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行,因此可以带来优化波动(扰动)。 不过从另一个方面来看,随机梯度下降所带来的波动有个好处就是,对于类似盆地区域 (即很多局部极小值点)那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点,这样便可能对于非凸函数,最终收敛于一个较好的局部极值点,甚至全局极值点。由于波动,因此会使得迭代次数(学习次数)增多,即收敛速度变慢。不过最终其会和全量梯度下降算法一样,具有相同的收敛性,即凸函数收敛于全局极值点,非凸损失函数收敛于局部极值点;
小批量梯度下降(Mini-Batch Gradient Descent)
Mini-batch 梯度下降综合了 batch 梯度下降与 stochastic 梯度下降,在每次更新速度与更新次数中间取得一个平衡,其每次更新从训练集中随机选择 batch_size,batch_size < m 个样本进行学习。相对于随机梯度下降算法,小批量梯度下降算法降低了收敛波动性, 即降低了参数更新的方差,使得更新更加稳定。相对于全量梯度下降,其提高了每次学习的速度。并且其不用担心内存瓶颈从而可以利用矩阵运算进行高效计算。一般而言每次更新随机选择[50,256]个样本进行学习,但是也要根据具体问题而选择,实践中可以进行多次试验, 选择一个更新速度与更次次数都较适合的样本数;
两种梯度下降法的示意图:

梯度下降法求解的例子:
- 先是全变量梯度下降
#%%全变量梯度下降
import numpy as np
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
#创建超参数
learning_rate = 0.001
n_lterations = 100000
n_epoches = 100 #学习100轮
#初始化w0 w1 ... 标准正太分布创建w
theta = np.random.randn(2,1)
for _ in range(n_lterations):
#求梯度,计算gradient
gradient = x_b.T.dot(x_b.dot(theta)-y) #gradient中每一行代表一个梯度
#应用梯度下降法公式去调整theta(直接采用矩阵运算)
theta = theta -learning_rate * gradient
print(theta)
- 接着是随机梯度下降
#%%随机梯度下降
import numpy as np
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
#创建超参数
learning_rate = 0.001
m = 100 #样本个数
n_epoches = 10000 #学习10000轮
#初始化w0 w1 ... 标准正太分布创建w
theta = np.random.randn(2,1)
for _ in range(n_epoches):
for _ in range(m):
random_index = np.random.randint(m)
xi = x_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradient = x_b.T.dot(x_b.dot(theta)-y)
theta = theta -learning_rate * gradient
print(theta)
- 小批量梯度下降
#%%小批量梯度下降
import numpy as np
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
#创建超参数
learning_rate = 0.001
n_epoches = 10000 #学习10000轮
batch_size = 10
num_batches = int(m/batch_size)
#初始化w0 w1 ... 标准正太分布创建w
theta = np.random.randn(2,1)
for _ in range(n_epoches):
for _ in range(num_batches):
random_index = np.random.randint(m)
x_batch = x_b[random_index:random_index+batch_size] #这里超出的索引不会报错,会切到最后一个为止
y_batch = y[random_index:random_index+batch_size]
gradient = x_b.T.dot(x_b.dot(theta)-y)
theta = theta -learning_rate * gradient
print(theta)
- 随机和小批量的改进(打乱顺序)
import numpy as np
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
#创建超参数
learning_rate = 0.001
m = 100 #样本个数
n_epoches = 10000 #学习10000轮
#初始化w0 w1 ... 标准正太分布创建w
theta = np.random.randn(2,1)
for _ in range(n_epoches):
#双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
arr = np.arange(len(x_b))
np.random.shuffle(arr) #打乱顺序
x_b = x_b[arr]
y = y[arr] #同时保证y也要打乱顺序
for i in range(m):
xi = x_b[i:i+1]
yi = y[i:i+1]
gradient = x_b.T.dot(x_b.dot(theta)-y)
theta = theta -learning_rate * gradient
print(theta)
print('*'*30)
#小批量改进
#创建超参数
learning_rate = 0.001
n_epoches = 10000 #学习10000轮
batch_size = 10
num_batches = int(m/batch_size)
#初始化w0 w1 ... 标准正太分布创建w
theta = np.random.randn(2,1)
for _ in range(n_epoches):
#双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
arr = np.arange(len(x_b))
np.random.shuffle(arr) #打乱顺序
x_b = x_b[arr]
y = y[arr] #同时保证y也要打乱顺序
for i in range(num_batches):
x_batch = x_b[i*batch_size:i*batch_size+batch_size] #这里超出的索引不会报错,会切到最后一个为止
y_batch = y[i*batch_size:i*batch_size+batch_size]
gradient = x_b.T.dot(x_b.dot(theta)-y)
theta = theta -learning_rate * gradient
print(theta)
#可以看出最终两者的结果是一样的
- 学习率的调整
import numpy as np
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
#创建超参数
# learning_rate = 0.001
#定义一个学习率调整的函数
t0,t1 = 5,500
def learning_rate_adj(t):
return t0/(t+t1)
n_lterations = 100000
n_epoches = 100 #学习100轮
#初始化w0 w1 ... 标准正太分布创建w
theta = np.random.randn(2,1)
for i in range(n_lterations):
learning_rate = learning_rate_adj(i)
#求梯度,计算gradient
gradient = x_b.T.dot(x_b.dot(theta)-y) #gradient中每一行代表一个梯度
#应用梯度下降法公式去调整theta(直接采用矩阵运算)
theta = theta -learning_rate * gradient
print(theta)
- 小批量改进
import numpy as np
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
#创建超参数
t0,t1 = 5,500
def learning_rate_adj(t):
return t0/(t+t1)
n_epoches = 10000 #学习10000轮
batch_size = 10
num_batches = int(m/batch_size)
#初始化w0 w1 ... 标准正太分布创建w
theta = np.random.randn(2,1)
for epoch in range(n_epoches):
#双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
arr = np.arange(len(x_b))
np.random.shuffle(arr) #打乱顺序
x_b = x_b[arr]
y = y[arr] #同时保证y也要打乱顺序
for i in range(num_batches):
learning_rate = learning_rate_adj(epoch*num_batches+i)
x_batch = x_b[i*batch_size:i*batch_size+batch_size] #这里超出的索引不会报错,会切到最后一个为止
y_batch = y[i*batch_size:i*batch_size+batch_size]
gradient = x_b.T.dot(x_b.dot(theta)-y)
theta = theta -learning_rate * gradient
print(theta)
消除伏笔
还记得前面关于$\varepsilon$的均值为0的假设吗? 现在我们来证明其实这个假设很合理, 而且在最小化Loss后, $\varepsilon$的均值就自然为0了:
代码如下:
#%% 验证残差项均值为0
import numpy as np
np.random.seed(2)
x = 2*np.random.rand(100,1)
#观察值 误差(服从正态分布)
y = 5 + 4*x + np.random.randn(100,1)
#为了求解w0的截距项,我们给x矩阵左边加上一列全为1的x0
x_b = np.concatenate((np.ones((100,1)),x),axis = 1)
w = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)
# 计算y_hat
y_pred = (w.T * x_b).sum(axis=1)
# 计算残差
e = y_pred - y
# 计算残差均值
e_mean = e.mean()
print('残差均值为:', e_mean)
输出值的量级为$10^{-15}$, 可以视为0了;
多元线性回归就是这样了, 继续下一章吧!pd的Machine Learning

