文本建模PLSA与LDA模型 -- 潘登同学的Machine Learning笔记

文本建模PLSA与LDA模型 -- 潘登同学的Machine Learning笔记

Unigram Model
n-gram model
PLSA模型(Probabilistic latent semantic analysis)
LDA 模型
- 为什么要选择这些分布

文本预处理-分词
LDA分析
结果展现
主题数目选择--困惑度

文本生成过程

一篇文档，可以看成是一组有序的词的序列 $d=(w_1,w_2,\ldots,w_n)$ . 从统计学角度来看，文档的生成可以看成是上帝抛掷骰子生成的结果，每一次抛掷骰子都生成一个词汇，抛掷N词生成一篇文档。在统计文本建模中，我们希望猜测出上帝是如何玩这个游戏的，这会涉及到两个最核心的问题：

上帝都有什么样的骰子；
上帝是如何抛掷这些骰子的；

第一个问题就是表示模型中都有哪些参数，骰子的每一个面的概率都对应于模型中的参数；第二个问题就表示游戏规则是什么，上帝可能有各种不同类型的骰子，上帝可以按照一定的规则抛掷这些骰子从而产生词序列。

Unigram Model

在Unigram Model中，我们采用词袋模型，假设了文档之间相互独立，文档中的词汇之间相互独立。假设我们的词典中一共有 V 个词 $v_1,v_2,\ldots,v_V$ ，那么最简单的 Unigram Model 就是认为上帝是按照如下的游戏规则产生文本的。

上帝只有一个骰子，这个骰子有V面，每个面对应一个词，各个面的概率不一；
每抛掷一次骰子，抛出的面就对应的产生一个词；如果一篇文档中N个词，就独立的抛掷n次骰子产生n个词；

n-gram model

对于n-gram model来说就是Unigram Model加了一个假设，假设当前词会受前n个词的影响，于是就用条件概率来生成词，那么n-gram model就是认为上帝是按照如下的游戏规则产生文本的。

上帝只有$C_V^n$个骰子，这个骰子有V面，每个面对应一个词，各个面的概率不一；
每抛掷一次骰子，抛出的面就对应的产生一个词；这个骰子会根据前n次抛掷的情况选择，这样N次，生成一篇文章

PLSA模型(Probabilistic latent semantic analysis)

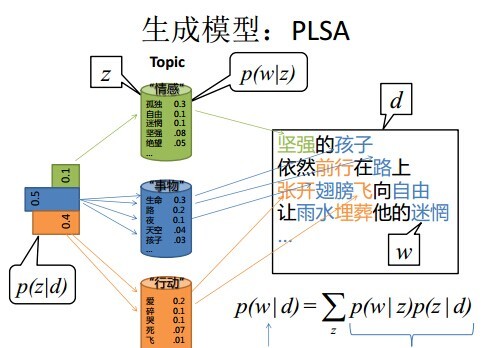
Unigram Model模型中，没有考虑主题词这个概念。我们人写文章时，写的文章都是关于某一个主题的，不是满天胡乱的写，比如一个财经记者写一篇报道，那么这篇文章大部分都是关于财经主题的，当然，也有很少一部分词汇会涉及到其他主题。所以，PLSA认为生成一篇文档的生成过程如下：

现有两种类型的骰子，一种是doc-topic骰子，每个doc-topic骰子有K个面，每个面一个topic的编号；一种是topic-word骰子，每个topic-word骰子有V个面，每个面对应一个词；
现有K个topic-word骰子，每个骰子有一个编号，编号从1到K；
生成每篇文档之前，先为这篇文章制造一个特定的doc-topic骰子，重复如下过程生成文档中的词： 3.1 投掷这个doc-topic骰子，得到一个topic编号z； 3.2 选择K个topic-word骰子中编号为z的那个，投掷这个骰子，得到一个词；

在这里插入图片描述

LDA 模型

生成文档步骤

按照先验概率$p(d_i)$选择一篇文档$d_i$
从Dirichlet分布$\alpha$中取样生成文档$d_i$的主题分布$\theta_i$，主题分布$\theta_i$由参数为$\alpha$的Dirichlet分布生成
从主题的多项式分布$\theta_i$中取样生成文档$d_i$第 j 个词的主题$z_{i,j}$
从Dirichlet分布$\beta$中取样生成主题$z_{i,j}$对应的词语分布$\phi_{z_{i,j}}$，词语分布$\phi_{z_{i,j}}$由参数为$\beta$的Dirichlet分布生成
从词语的多项式分布$\phi_{z_{i,j}}$中采样最终生成词语$w_{i,z}$

在这里插入图片描述

下图可以加深对上面的理解

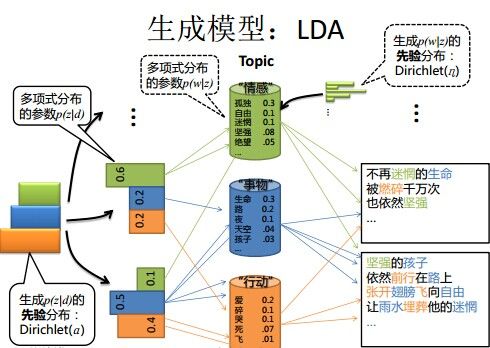
为什么要选择这些分布

为什么选择狄利克雷(Dirichlet)分布作为先验分布，因为待估计的总体分布是多项分布，将先验分布选择为狄利克雷(Dirichlet)分布，那么后验分布也就是狄利克雷(Dirichlet)分布，在做极大似然时候就方便计算；这里的重要概念是共轭先验分布；共轭先验分布在数量统计里面讲过，对于一个共轭先验分布用简单的数学表达就是 $$ P(\theta|x) = \frac{P(\theta,x)}{P(x)}，其中P(\theta|x)、P(\theta,x)都服从同一分布(可能参数不同) $$

下图通过概率图的形式描述了这一过程