命名实体识别BiLSTM-CRF代码实现 -- 潘登同学的NLP笔记
条件随机场概述
条件随机场(Conditional Random Fields),是在给定一组输入随机变量条件下另外一组输出随机变量的条件概率分布模型,它是一种判别式的概率无向图模型,既然是判别式,拿就是对条件概率分布建模;
之前也在BiLSTM-CRF中聊过,判别式模型就是给定x计算y,生成式模型就是计算联合分布的参数;
设有线性链结构的随机变量序列 $X=(X_1,X_2,...,X_n),Y=(Y_1,Y_2,...,Y_N)$,在给定观察序列 $X$ 的条件下,随机变量序列 $Y$ 的条件概率分布为 $P(Y|X)$,若其满足马尔科夫特性,即 $$ P(Yi|X,Y1,Y2...Yn)=P(Yi|X,Yi−1,Yi+1) $$ 这时 $P(Y|X)$ 则为线性链条件随机场
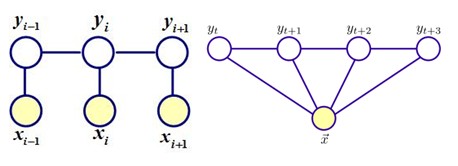
条件随机场(ConditionalRandom Field,CRF)是经典 NER 的主流模型。
- 它的目标函数不仅考虑输入的状态特征函数,而且还包含了标签转移特征函数。
- 在训练时可以使用 SGD 学习模型参数。
- 在已知模型时,给输入序列求预测输出序列即求使目标函数最大化的最优序列,是一个动态规划问题,可以使用 Viterbi 算法解码来得到最优标签序列。
- CRF 的优点在于其为一个位置进行标注的过程中可以利用丰富的内部及上下文特征信息。
直观的例子
假设你有许多小明同学一天内不同时段的照片,从小明提裤子起床到脱裤子睡觉各个时间段都有(小明是照片控!)。现在的任务是对这些照片进行分类。比如有的照片是吃饭,那就给它打上吃饭的标签;有的照片是跑步时拍的,那就打上跑步的标签;有的照片是开会时拍的,那就打上开会的标签。问题来了,你准备怎么干?
一个简单直观的办法就是,不管这些照片之间的时间顺序,想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据,训练出一个模型,直接根据照片的特征来分类。例如,如果照片是早上 6:00 拍的,且画面是黑暗的,那就给它打上睡觉的标签;如果照片上有车,那就给它打上开车的标签。这样可行吗?
乍一看可以!但实际上,由于我们忽略了这些照片之间的时间顺序这一重要信息,我们的分类器会有缺陷的。举个例子,假如有一张小明闭着嘴的照片,怎么分类?显然难以直接判断,需要参考闭嘴之前的照片,如果之前的照片显示小明在吃饭,那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽,可以给它打上吃饭的标签;如果之前的照片显示小明在唱歌,那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍,可以给它打上唱歌的标签。所以,为了让我们的分类器能够有更好的表现,在为一张照片分类时,我们必须将与它相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方!
CRF的特征函数们
我们正式地定义一下什么是 CRF 中的特征函数,所谓特征函数,就是这样的函数,它接受四个参数:
- 句子 $s$(就是我们要标注词性的句子)
- $i$,用来表示句子 $s$ 中第 $i$ 个单词
- $l_i$,表示要评分的标注序列给第 $i$ 个单词标注的词性
- $l_i-1$,表示要评分的标注序列给第 $i-1$ 个单词标注的词性 它的输出值是 0 或者 1,0 表示要评分的标注序列不符合这个特征,1 表示要评分的标注序列符合这个特征
注意: 这里,我们的特征函数仅仅依靠当前单词的标签和它前面的单词的标签对标注序列进行评判,这样建立的 CRF 也叫作线性链 CRF,这是 CRF 中的一种简单情况。为简单起见,本文中我们仅考虑线性链 CRF
最终算法的预测值$\hat{y_i}$受很多个特征函数的影响,写为数学表达式 $$ \begin{aligned} P(y|x) &= \frac{P_{RealPath}}{TotalPath} = \frac{e^{S_i}}{Z(x)} \ &= \frac{1}{Z(x)}\exp(\sum_{i,k} \lambda_k \cdot t_k (y_i,y_{i-1},x,i) + \sum_{i,l} \mu_k \cdot e_l (y_i,x,i)) \end{aligned} $$
其中$x$与$s$表达意思一致, $\lambda_k$为transition scores矩阵的一个元素,$t_k$为特征函数,特征函数个数与$\lambda_k$都是$label^2$个; 既然前面是transition scores的一个表达,那么后面自然是Emission scores的表达,$e_l$也理解为特征函数;exp中的是某一条路径中的表达式;$Z(x)$则是所有路径的加和...
举些例子
$$ f_1(s,i,l_i,l_{i-1}) = 1 $$ 当 $l_i$ 是“副词”并且第 $i$ 个单词以“ly”结尾时,我们就让 $f_1 = 1$,其他情况 f1 为 0。不难想到,$f_1$ 特征函数的权重$\lambda_1$ 应当是正的。而且$\lambda_1$ 越大,表示我们越倾向于采用那些把以“ly”结尾的单词标注为“副词”的标注序列;
$$ f_2(s,i,l_i,l_{i-1}) = 1 $$ 如果 $i=1$,$l_i=动词$,并且句子 $s$ 是以“?”结尾时,$f_2=1$,其他情况 $f_2=0$。同样,$\lambda_2$ 应当是正的,并且$\lambda_2$ 越大,表示我们越倾向于采用那些把问句的第一个单词标注为“动词”的标注序列;
$$ f_3(s,i,l_i,l_{i-1}) = 1 $$ 当 $l_{i-1}$ 是介词,$l_i$ 是名词时,$f_3 = 1$,其他情况 $f_3=0$。$\lambda_3$ 也应当是正的,并且$\lambda_3$ 越大,说明我们越认为介词后面应当跟一个名词;
$$ f_3(s,i,l_i,l_{i-1}) = 1 $$ 如果 $l_i$ 和 $l_{i-1}$ 都是介词,那么 $f_4$ 等于 1,其他情况 $f_4=0$。这里,我们应当可以想到$\lambda_4$ 是负的,并且$\lambda_4$ 的绝对值越大,表示我们越不认可介词后面还是介词的标注序列;
对比逻辑回归
CRF的概率形式与softmax很像,softmax又是逻辑回归的推广 $$ p(l|s) = \frac{\exp{[\sum_{j=1}^m \sum_{i=1}^n f_j (l_i,l_{i-1},s,i)}]}{\sum \exp{[\sum_{j=1}^m \sum_{i=1}^n f_j (l_i,l_{i-1},s,i)]}} $$ 那是因为 CRF 确实基本上是逻辑回归的序列版本,鉴于逻辑回归是一个对数线性模型用于分类,CRF 是一个对数线性模型用于序列打标签
对比HMM
HMM 采用生成式方法去打标签,数学表达为 $$ p(l,s) = p(l_1)\prod_i p(l_i|l_{i-1})p(w_i|l_i) $$ CRF 更强大,它可以做 HMM 可以完成的一切,并且还能做 HMM 不能做的, 我们将HMM的表达式往CRF上靠 $$ \log p(l,s) = \log p(l_1) + \sum_i\log p(l_i|l_{i-1}) + \sum_i\log p(w_i|l_i) $$ 如果我们考虑这些对数概率为相对应的二元的转化和发射指标特征的权重。即,我们可以构建一个 CRF 等同于任意 HMM, 对于每个HMM的转移概率$\log p(l_i=y|l_{i-1}=x)$,可以理解为只有两个输入的特征函数,每个特征函数的权重为$w_{x,y} = \log p(l_i=y|l_{i-1}=x)$每个特征函数的输出都是1;
类似地,对于每个 HMM 的发射概率$\log p(w_i|l_i)$,也可以视作特征函数,每个特征函数的权重为$w_{x,z} = \log p(w_i=z|l_{i}=x)$;
因此,由 CRF 计算的分数 p(l|s)使用这些特征函数是精确地成比例的对应于 HMM 计算的分数,所以每一个 HMM 是等同于一些 CRF的特征函数;
CRFs 可以建模更丰富的标签分布,这里有两个原因:
- CRFs 可以定义更大的特征集合。然后 HMMs 必然是局部在本质上(因为它们被限制到二元的转换和发射特征函数,强迫每个单词仅依赖于当前的标签和每个标签仅依赖于之前的标签),CRFs 可以使用更多全局的特征。例如,一个特征在我们的 POS 标签的概率增长,一个句子首个单词标注为动词如果句子最后包含一个问号符号。
- CRFs可以有任意的权重 。 鉴于 HMM 的概率必须满足某些限制, 例如$0<=p(w_i|l_i)<=1,\sum_w P(w_i=w|l_i)=1$,但CRF 的权重是不限制的;
HMM模型存在两个严格假设:
- 输出观察值之间严格独立(之前概率图中的head-to-tail)
- 状态的转移过程中当前状态只与前一状态有关(一阶马尔科夫模型)
除此之外,HMM还会出现标注偏置问题:
- 假设有三个状态(标签)a,b,c
- 在语料库训练中,a转移到b的概率,大于a转移到c的概率(统计出来的),所以很受语料库统计的影响,可能会造成HMM在测试的时候只出现a到b的状态
Bilstm-CRF命名实体识别代码实现
数据预处理

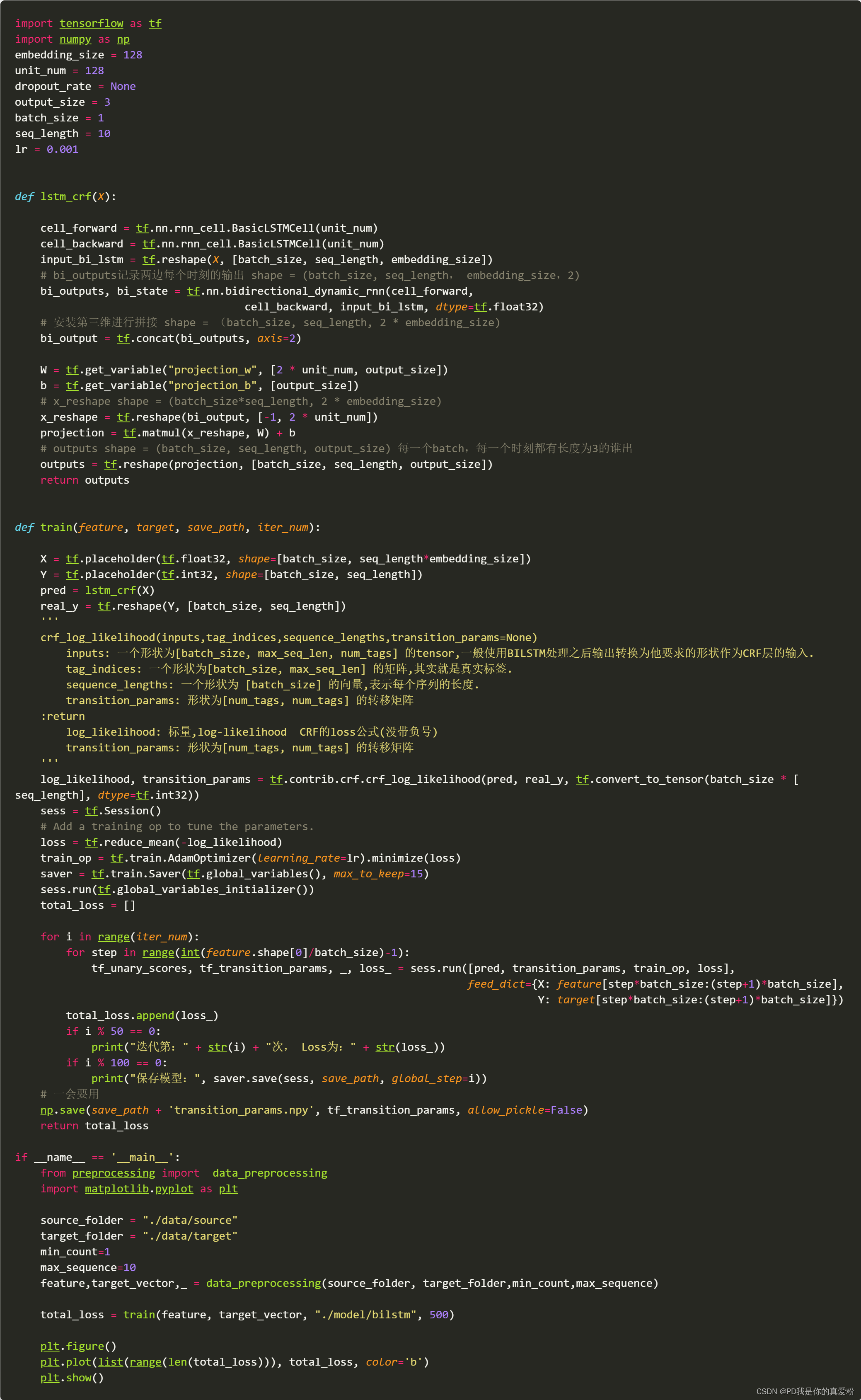
训练模型
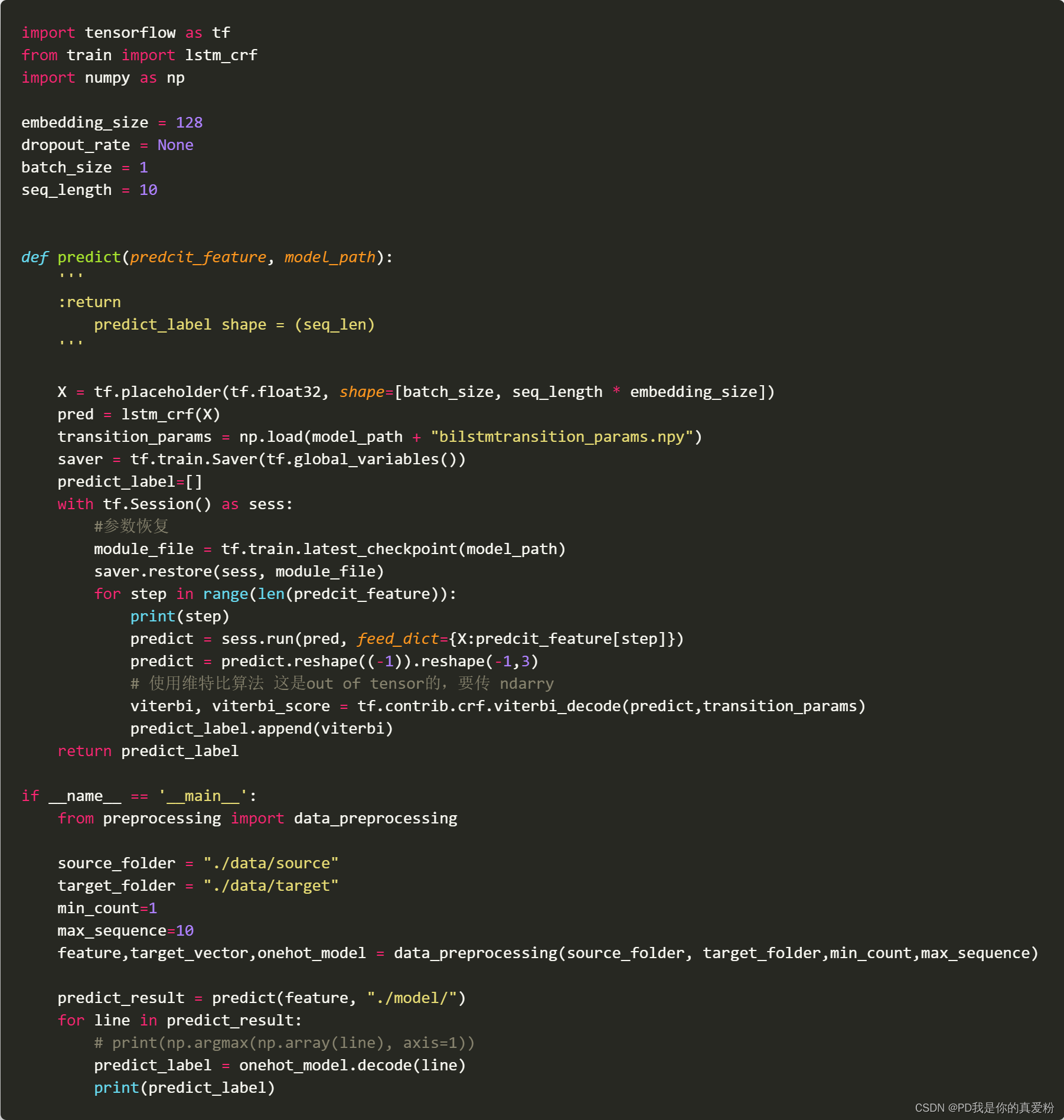
模型应用(维特比算法)